��Ŀ����
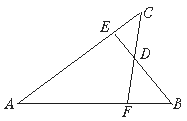
����Ŀ����ij��������ͼ����ʾ�ij����κ�������ֽ��������ͼ����ʾ�� A��B ���ֳ�������״����ֽ��.�� ��������ֽ�� 120 �ţ�������ֽ�� 360 �ţ��պ�ȫ�����꣬�������ɶ��ٸ� A �ͺ��ӣ��������н��� ��ȷ�ĸ����ǣ� ��

�ټ�ͬѧ���� A �ͺ��Ӹ���Ϊ x ������������ɵã� 4x 3 ![]() 360
360
����ͬѧ���� B �ͺ���������ֽ��ĸ���Ϊ m ������������ɵã� 3 ![]() 4(120 m) 360
4(120 m) 360
��A �ͺ� 72 ��
��B �ͺ���������ֽ�� 48 ��
A.1B.2C.3D.4
���𰸡�D
��������
���������֪��A��ֽ����Ҫ4��������ֽ�壬1��������ֽ�壬B��ֽ����Ҫ3��������ֽ���2��������ֽ�壬��A�ͺ��Ӹ���Ϊx�����ɵ�A��ֽ����Ҫ������ֽ���������B��ֽ����Ҫ������ֽ������������г����̶Ԣٽ����жϣ���B�ͺ���������ֽ��ĸ���Ϊm�����ɵ�B��ֽ����Ҫ������ֽ���������A��ֽ����Ҫ������ֽ������������г����̶Ԣڽ����жϣ�����A�ͺ�������������ֽ��x�ţ���B�ͺ�������������ֽ��y�ţ���ɵ�A�ͺ���x����B�ͺ���y�������ݳ�����ֽ��360�ţ�������ֽ��120�ţ��ɵó������飬���A��ֽ�к�B��ֽ�е������ɶԢۢܽ����жϣ�
��A�ͺ��Ӹ���Ϊx������A��ֽ����Ҫ������ֽ��4x�ţ�������ֽ��x�ţ���������һ��B��ֽ����Ҫ����������ֽ�壬��˿ɵ�B��ֽ�е�����Ϊ![]() ������Ҫ������ֽ��3��
������Ҫ������ֽ��3��![]() �ţ���˿ɵ�
�ţ���˿ɵ�![]() ���ʢ���ȷ��
���ʢ���ȷ��
��B�ͺ���������ֽ��ĸ���Ϊm������B��ֽ����![]() ������Ҫ������ֽ��3��
������Ҫ������ֽ��3��![]() ����A��ֽ���У�120-m���������賤����ֽ��4��120-m���������Կɵ÷���3��
����A��ֽ���У�120-m���������賤����ֽ��4��120-m���������Կɵ÷���3��![]() +4��120-m��=120���ʢ���ȷ��
+4��120-m��=120���ʢ���ȷ��
����A�ͺ�������������ֽ��x�ţ���B�ͺ�������������ֽ��y�ţ����У�
![]()
��ã�![]()
����A��ֽ����72����B��ֽ����24��������B �ͺ���������ֽ�� 48 ��
�ʢۢ���ȷ.
��ѡD.

 ��У����ϵ�д�
��У����ϵ�д�