题目内容
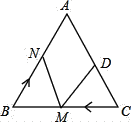
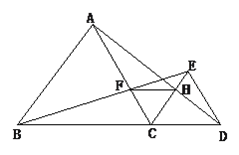
【题目】如图,已知点B、C、D在同一条直线上,△ABC和△CDE都是等边三角形.BE交AC于F,AD交CE于H,
①求证:△BCE≌△ACD;
②求证:CF=CH;
③判断△CFH的形状并说明理由。
【答案】①证明见解析②证明△BCF≌△ACH;③△CFH是等边三角形
【解析】试题分析:①利用等边三角形的性质得出条件,可证明:△BCE≌△ACD;
②利用△BCE≌△ACD得出∠CBF=∠CAH,再运用平角定义得出∠BCF=∠ACH进而得出△BCF≌△ACH因此CF=CH.
③由CF=CH和∠ACH=60°根据“有一个角是60°的三角形是等边三角形可得△CFH是等边三角形.
试题解析:①证明:∵∠BCA=∠DCE=60°,
∴∠BCE=∠ACD.
又BC=AC、CE=CD,
∴△BCE≌△ACD.
②∵△BCE≌△ACD,
∴∠CBF=∠CAH.
∵∠ACB=∠DCE=60°,
∴∠ACH=60°.
∴∠BCF=∠ACH.
又BC=AC,
∴△BCF≌△ACH.
∴CF=CH.
③∵CF=CH,∠ACH=60°,
∴△CFH是等边三角形.

练习册系列答案
 点睛新教材全能解读系列答案
点睛新教材全能解读系列答案 小学教材完全解读系列答案
小学教材完全解读系列答案
相关题目