题目内容
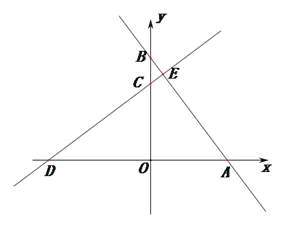
【题目】(本题满分12分) 在平面直角坐标系中,直线![]() 交
交![]() 轴、
轴、![]() 轴分别于点
轴分别于点![]() 、点
、点![]() ,将△
,将△![]() 绕坐标原点逆时针旋转
绕坐标原点逆时针旋转![]() 得到△
得到△![]() .直线
.直线![]() 交直线
交直线![]() 于点
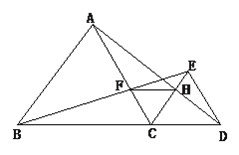
于点![]() ,如图1.
,如图1.
(1))求:直线![]() 的函数关系式.
的函数关系式.
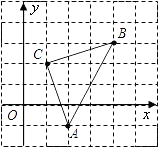
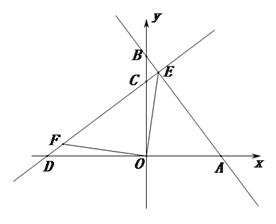
(2)如图2,连接![]() ,过点
,过点![]() 作
作![]() 交直线
交直线![]() 于点
于点![]() ,如图2.
,如图2.
① 求证: ![]() =
=![]() .
.
② 求:点![]() 的坐标.
的坐标.
(3)若点![]() 是直线
是直线![]() 上一点,点
上一点,点![]() 是
是![]() 轴上一点(点
轴上一点(点![]() 不与点
不与点![]() 重合),当△
重合),当△![]() 和△
和△![]() 全等时,直接写出点
全等时,直接写出点![]() 的坐标.
的坐标.
![]()
![]()
【答案】(1)![]() (2)①见解析;②
(2)①见解析;②![]() ;(3)
;(3)![]() ,
, ![]() ,
, ![]()
【解析】试题分析:(1)先求出A,B点坐标,根据旋转90°,再求出C,D点坐标,待定系数法求一元一次函数.
(2) ①先证△DFO≌△BOE,可得OF=OE , 再利用等边对等角,求得∠OEF=45°.
② 先联立方程组,求点E(![]() 再构造全等,求出点F (
再构造全等,求出点F (![]() ).
).
(3)利用全等和中点坐标公式,可求得P点坐标,P点有多解情况,要分类讨论.
试题解析:
![]() ,
,
令x=0,B(0,4),令y=0,A(3,0),则D(-4,0),C(0, ![]()
解设过D,C直线解析式是![]() ,
,
![]() ,
,
解得 ,
,
![]() .
.
(2)①![]() ,
,
![]()
![]() ,
,
△![]() 旋转了90°,所以
旋转了90°,所以![]() ,
, ![]() ,
,
 ,
,
![]() △DFO≌△BOE,可得OF=OE ,
△DFO≌△BOE,可得OF=OE ,
![]() ∠OEF=45°.
∠OEF=45°.
②联立,解得E(
![]() ,由①知,△DFO≌△BOE,
,由①知,△DFO≌△BOE,
所以旋转以后得F (![]() ).
).
P(-8,-3 ),( ![]() ,(
,( ![]()

如图,与![]() CDO面积相等(也就是全等)满足题意的三角形有三个,
CDO面积相等(也就是全等)满足题意的三角形有三个,
在![]() ,,D(-4,0)点是C(0,3)和
,,D(-4,0)点是C(0,3)和![]() 中点,
中点, ![]() ,
,![]() ,
,
所以有![]() ,
,
在![]() ,由题意知
,由题意知![]() ,(1,0),OD=O
,(1,0),OD=O![]() ,勾股定理知,P3纵坐标
,勾股定理知,P3纵坐标![]() ,代入直线
,代入直线![]() ,得到P3(
,得到P3(![]() ))
))
在![]() 由题意知D(-4,0)是
由题意知D(-4,0)是![]() (x,y),P3(
(x,y),P3(![]() )中点,
)中点, ![]() =-4,
=-4, ![]() =0,
=0,  ,
,
所以![]() ,
,
所以P的坐标是, ![]() ,
, ![]() ,
, ![]() .
.

练习册系列答案
 名校课堂系列答案
名校课堂系列答案
相关题目