��Ŀ����
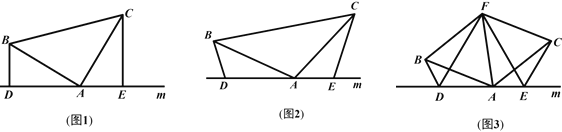
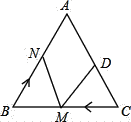
����Ŀ����ͼ���ڵȱ���ABC�У�AB=AC=BC=10���ף�DC=4���ף������M��3����/����ٶ��˶���
��1�������M���߶�CB���ɵ�C���B�˶�����N���߶�BA����B����A���˶�������ͬʱ����������N���˶��ٶ����M���˶��ٶ���ȣ�
�پ���2�����BMN����CDM�Ƿ�ȫ�ȣ���˵�����ɣ�
�ڵ�������˶�ʱ��Ϊ����ʱ����BMN��һ��ֱ�������Σ�
��2������N���˶��ٶ����M���˶��ٶȲ���ȣ���N�ӵ�B��������M��ԭ�����˶��ٶȴӵ�Cͬʱ��������˳ʱ������ABC�����˶�������25���M���N��һ�����������N���˶��ٶ����� ������/�룮��ֱ��д���𰸣�
���𰸡���1������BMN�ա�CDM�����ɼ��������ڵ�t=![]() ���t=
���t=![]() ��ʱ����BMN��ֱ�������Σ���2��3.8��2.6��
��ʱ����BMN��ֱ�������Σ���2��3.8��2.6��
������������������ٸ��������CM=BN=6CM������BM=4CM=CD�����ݡ�SAS��֤����BMN�ա�CDM��
�����˶�ʱ��Ϊt�룬�ֱ��ʾCM��BN��������������������������ε�������⣺I����NMB=90�㣻��BNM=90�㣻
��2����M���N��һ�������������ֿ��ܣ�I����M�˶��ٶȿ죻��N�˶��ٶȿ죮�ֱ��з�����⣮
�����������1���١�BMN�ա�CDM���������£�
��VN=VM=3����/�룬��t=2�룬
��CM=2��3=6��cm����
BN=2��3=6��cm����
BM=BC��CM=10��6=4��cm����
��BN=CM��
��CD=4��cm����
��BM=CD��
����ABC�ǵȱ������Σ�
���B=��C=60�㣬
����BMN����CDM��
BN=CM����B=��C��BM=CD��
���BMN�ա�CDM����SAS��.
�����˶�ʱ��Ϊt�룬��BMN��ֱ�������������������
����NMB=90��ʱ��
�ߡ�B=60�㣬
���BNM=90�㩁��B=90�㩁60��=30�㣮
��BN=2BM��
��3t=2����10��3t����
��t=![]() ���룩��
���룩��
����BNM=90��ʱ��
�ߡ�B=60�㣬
���BMN=90�㩁��B=90�㩁60��=30�㣮
��BM=2BN��
��10��3t=2��3t��
��t=![]() ���룩��
���룩��
�൱t=![]() ���t=
���t=![]() ��ʱ����BMN��ֱ�������Σ�
��ʱ����BMN��ֱ�������Σ�
��2��������������ۣ�
I������M�˶��ٶȿ죬�� 3��25��10=25VN����� VN=2.6��
������N�˶��ٶȿ죬�� 25VN��20=3��25����� VN=3.8��
�ʴ�Ϊ 3.8��2.6��