Question

【题目】在边长为2的正方形ABCD中，P为AB上的一动点，E为AD中点，PE交CD延长线于Q，过E作EF⊥PQ交BC的延长线于F，则下列结论：①△APE≌△DQE；②PQ=EF；③当P为AB中点时，CF=；④若H为QC的中点，当P从A移动到B时，线段EH扫过的面积为1，其中正确的有（ ）

A.1个B.2个C.3个D.4个

Answer 1

【答案】B

【解析】

根据正方形的性质、全等三角形的性质、勾股定理、三角形面积公式一一判断即可．

①∵四边形ABCD是正方形，

∴AB=BC=CD=AD，∠A=∠B=90°，

∵∠A=∠EDQ，∠AEP=∠QED，AE=ED，

∴△AEP≌△DEQ，故①正确，

②作PG⊥CD于G，EM⊥BC于M，

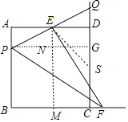
∴∠PGQ=∠EMF=90°，

∵EF⊥PQ，

∴∠PEF=90°，

∴∠PEN+∠NEF=90°，

∵∠NPE+∠NEP=90°，

∴∠NPE=∠NEF，

∵PG=EM，

∴△EFM≌△PQG，

∴EF=PQ，故②正确，

③连接QF．则QF=PF，PB2+BF2=QC2+CF2，设CF=x，则（2+x）2+12=32+x2，

∴x=1，故③错误，

④当P在A点时，Q与D重合，QC的中点H在DC的中点S处，

当P运动到B时，QC的中点H与D重合，

故EH扫过的面积为△ESD的面积的一半为，故④错误．

故选：B．