Question

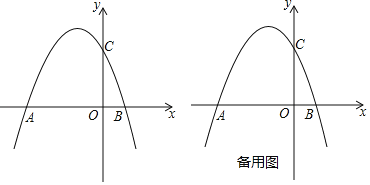
【题目】如图，抛物线y＝﹣x2+bx+c交x轴于A、B两点，其中点A坐标为(﹣3，0)，与y轴交于点C(0，3)．

（1）求抛物线的函数解析式；

（2）点M为抛物线y＝﹣x2+bx+c上异于点C的一个点，且S△OMC＝S△ABC，求点M的坐标；

（3）若点P为x轴上方抛物线上任意一点，点D是抛物线对称轴与x轴的交点，直线AP、BP分别交抛物线的对称轴于点E、F．请问DE+DF是否为定值？如果是，请求出这个定值；如果不是，请说明理由．

Answer 1

【答案】（1）y＝﹣x2﹣2x+3；（2）(2，﹣5)或(﹣2，3)；（3）是定值，8

【解析】

（1）将点A、C的坐标代入抛物线表达式，即可求解；

（2）S△ABC＝××AB×OC＝×4×3＝3，而S△OMC＝×OC×||＝||＝3，即可求解；

（3）求出直线AP、BP的函数表达式，即可求解．

解：（1）将点A、C的坐标代入抛物线表达式得，解得，

故抛物线的表达式为：y＝﹣x2﹣2x+3；

（2）对于抛物线y＝﹣x2﹣2x+3，令y＝0，则x＝﹣3或1，

故点B（1，0），

∴S△ABC＝××AB×OC＝×4×3＝3，

∵S△OMC＝×OC×||＝||＝3，解得：＝±2，

故点M的坐标为（2，﹣5）或（﹣2，3）；

（3）是定值，理由：

设点P的坐标为（m，﹣m2﹣2m+3），

设直线AP的表达式为：y＝kx+t，则，解得，

故直线AP的表达式为：y＝﹣（m﹣1）（x+3），

当x＝＝﹣1时，y＝2﹣2m，即点E（﹣1，2﹣2m），即DE＝2﹣2m，

同理可得，直线BP的表达式为：y＝﹣（m+3）（x﹣1），

当x＝﹣1时，y＝2m+6，故点F（﹣1，2m+6），即DF＝2m+6，

∴DE+DF＝2﹣2m+2m+6＝8，为定值．