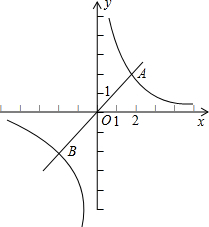题目内容
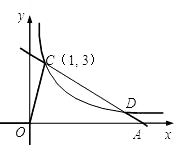
如图,直线经过A(1,0),B(0,1)两点,点P是双曲线y=
(x>0)上任意一点,PM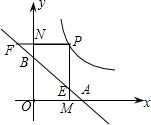 ⊥x轴,PN⊥y轴,垂足分别为M,N.PM与直线AB交于点E,PN的延长线与直线AB交于点F.
⊥x轴,PN⊥y轴,垂足分别为M,N.PM与直线AB交于点E,PN的延长线与直线AB交于点F.
(1)求证:AF•BE=1;
(2)若平行于AB的直线与双曲线只有一个公共点,求公共点的坐标.
| 1 |
| 2x |
 ⊥x轴,PN⊥y轴,垂足分别为M,N.PM与直线AB交于点E,PN的延长线与直线AB交于点F.
⊥x轴,PN⊥y轴,垂足分别为M,N.PM与直线AB交于点E,PN的延长线与直线AB交于点F.(1)求证:AF•BE=1;
(2)若平行于AB的直线与双曲线只有一个公共点,求公共点的坐标.
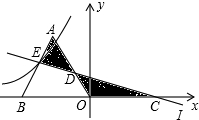
(1)证明:过点E、F分别作y轴、x轴的垂线,垂足为D、C,
则△AOB,△FCA,△DBE为等腰直角三角形,
设P(x0,y0),则FC=y0,DE=x0,AF=
y0,BE=
x0,
∴AF•BE=
y0•
x0=2x0y0,
又y0=
,
即2x0y0=1,
∴AF•BE=1;
(2)平行于AB的直线l的解析式为y=-x+b,设l与双曲线的唯一公共点Q坐标为(x,y),
联立
,得2x2-2bx+1=0,
由△=4b2-8=0,得b=
(-
舍去),
∴x=
,y=
,
即Q点的坐标为(
,
).

则△AOB,△FCA,△DBE为等腰直角三角形,
设P(x0,y0),则FC=y0,DE=x0,AF=
| 2 |
| 2 |
∴AF•BE=
| 2 |
| 2 |
又y0=
| 1 |
| 2x0 |
即2x0y0=1,
∴AF•BE=1;
(2)平行于AB的直线l的解析式为y=-x+b,设l与双曲线的唯一公共点Q坐标为(x,y),
联立
|
由△=4b2-8=0,得b=
| 2 |
| 2 |
∴x=
| ||
| 2 |
| ||
| 2 |
即Q点的坐标为(
| ||
| 2 |
| ||
| 2 |


练习册系列答案
 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案 目标测试系列答案
目标测试系列答案
相关题目