题目内容
【题目】如图1,△ABC和△DEF是两块可完全重合的三角板,![]() ,
,![]() .在如图1所示的状态下,△DEF固定不动,将△ABC沿直线a向左平移.
.在如图1所示的状态下,△DEF固定不动,将△ABC沿直线a向左平移.
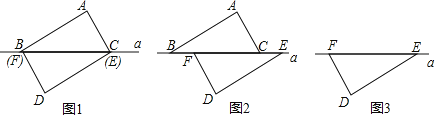
(1)当△ABC移到图2位置时,连解AF、DC,求证:AF=DC;
(2)若EF=8,在上述平移过程中,试猜想点C距点E多远时,线段AD被直线a垂直平分。并证明你的猜想是正确的。
【答案】(1)见解析;(2)当点C距点E的距离为4时,理由见解析.
【解析】
(1)连接AF,CD,由BC=EF,得到BF=CE,证明△ABF≌△DEC,得到AF=DC.
(2)当点C距点E的距离为4时,线段AD被直线a垂直平分,利用直角三角形的性质,进行解答即可.
(1)如图2,连接AF,CD,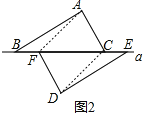
∵BC=EF,
∴BC-FC=EF-FC,
即BF=CE,
在△ABF和△DEC中,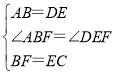 ,
,
∴△ABF≌△DEC,
∴AF=DC.
(2)当点C距点E的距离为4时,线段AD被直线a垂直平分,
证明:如图3,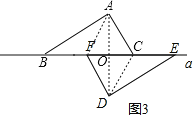
∵AF=DC,AC=DF,
∴四边形AFDC是平行四边形,
若AD被直线a垂直平分,假设a与AD交于点O,
在Rt△EFD中,∠DEF=30°
∴DF=![]() EF=4,
EF=4,
在Rt△FDO中,∠FDO=30°,
∴OF=![]() DF=2,
DF=2,
∴OC=2,
∴CE=EF-OF-OC=8-2-2=4.

练习册系列答案
相关题目