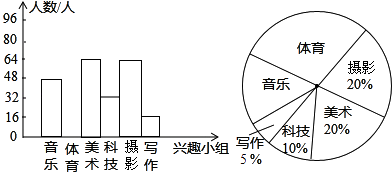
题目内容
【题目】如图,四边形ABCD中,AD∥BC,∠A=120°,BD平分∠ABC.
(1)若BD⊥CD,求∠C的度数;
(2)射线AP从AB位置开始,以每秒10°的速度绕点A逆时针旋转,6秒后AP与BD有何种位置关系?并说明理由.
(3)在(2)的条件下,AP旋转一圈回到AB处时停止运动,若射线AP与直线BD相交所成的角中较小的角为x°,当10<x<20,则旋转时间t(单位:秒)的取值范围是 .
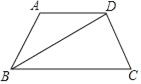
【答案】(1)∠C=60°;(2)PA⊥BD,理由见解析;(3)13<t <14.
【解析】
(1)在Rt△BDC中,求出∠DBC即可;
(2)结论:PA⊥BD.如图2中,设AP交BD于H.只要证明∠AHB=90°即可;
(3)如图3中,①当∠APD=20°时,易知∠DAP=30°﹣20°=10°,推出∠BAP=130°,此时t=13秒.②当∠AP′D=10°时,易知∠DAP′=30°﹣10°=20°,推出∠BAP=140°,此时t=14秒,由此即可判断.
解:(1)如图1中,
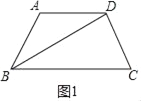
∵AD∥BC,BD平分∠ABC,
∴∠ADB=∠DBC=∠ABD,
∵∠A=120°,
∴∠ABD=∠ADB=∠DBC=30°,
∵BD⊥CD,
∴∠BDC=90°,
∴∠C=90°﹣∠DBC=60°;
(2)结论:PA⊥BD.
理由:如图2中,设AP交BD于H.
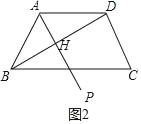
由题意∠BAP=6×10°=60°,
∵∠ABD=30°,
∴∠BAP+∠ABD=90°,
∴∠AHB=90°,
∴AP⊥BD.
(3)如图3中,
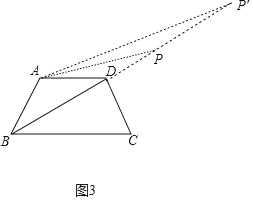
①当∠APD=20°时,易知∠DAP=30°﹣20°=10°,
∴∠BAP=130°,
此时t=13秒.
②当∠AP′D=10°时,易知∠DAP′=30°﹣10°=20°,
∴∠BAP=140°,
此时t=14秒,
∴当13<t<14时,10<x<20.
故答案为:(1)∠C=60°;(2)PA⊥BD,理由见解析;(3)13<t <14.

 孟建平小学滚动测试系列答案
孟建平小学滚动测试系列答案 黄冈天天练口算题卡系列答案
黄冈天天练口算题卡系列答案【题目】如图是连续十周测试甲、乙两名运动员体能情况的折线统计图,教练组规定:体能测试成绩70分以上(包括70分)为合适.
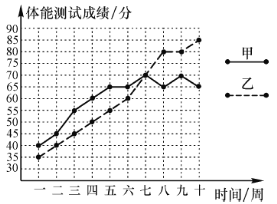
(1)请根据图中所提供的信息填写下表:
平均数 | 中位数 | 体能测试成绩合格次数(次) | |
甲 | 65 | ||
乙 | 60 |
(2)请从下面两个不同的角度对运动员体能测试结果进行判断:①依据平均数与成绩合格的次数比较甲和乙,哪个的体能测试成绩较好;②依据平均数与中位数比较甲和乙,哪个的体能测试成绩较好;
(3)依据折线统计图和成绩合格的次数,分析哪位运动员体能训练的效果较好.