题目内容
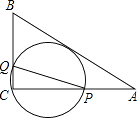
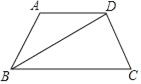
【题目】请你补全证明过程:如图,DG⊥BC,AC⊥BC,EF⊥AB,∠1=∠2,求证:EF∥CD

证明:∵DG⊥BC,AC⊥BC(已知)
∴∠DGB=90°,∠ACB=90°①( )
∴∠DGB=∠ACB ②( )
∴DG∥AC ③( )
∴∠2= ④________ ⑤( )
又∠1=∠2 ⑥( )
∴∠1=∠DCA ⑦( )
∴EF∥CD ⑧( )
【答案】①垂直的定义,②等量代换,③同位角相等,两直线平行,④∠DCA,⑤两直线平行,内错角相等,⑥已知, ⑦等量代换,⑧同位角相等,两直线平行
【解析】
先根据垂直的定义得出∠DGB=∠ACB,再由平行线的判定定理得出DG∥AC,故可得出∠2=∠DCA,利用等量代换得出∠1=∠DCA,进而可得出结论.
证明:∵DG⊥BC,AC⊥BC(已知) ,
∴∠DGB=90°,∠ACB=90°(垂直的定义),
∴∠DGB=∠ACB (等量代换) ,
∴DG∥AC (同位角相等,两直线平行) ,
∴∠2=∠DCA(两直线平行,内错角相等),
又∠1=∠2(已知),
∴∠1=∠DCA(等量代换),
∴EF∥CD(同位角相等,两直线平行).

练习册系列答案
相关题目