题目内容
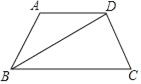
【题目】在□ABCD中，AD=BD，BE是AD边上的高，∠EBD=28°，则∠A的度数为_______.
【答案】59°或31°
【解析】
分析题意，首先根据已知作出图，由于△ABD的形状不确定，故需分类讨论：
当E点在线段AD上时，首先求出∠ADB的度数，再利用三角形内角和定理以及等腰三角形的性质，得出∠A的度数；
当E点在AD的延长线上时，结合已知可先求出∠BDE的度数，然后根据等腰三角形的性质以及三角形外角的性质进行求解即可
情况一：当E点在线段AD上时，如图所示：
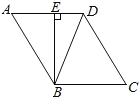
∵BE是AD边上的高，∠EBD=28°，
∴∠ADB=90°-28°=62°.
∵AD=BD，
∴∠A=∠ABD=(180°-62°)÷2=59°.
情况二：当E点在AD的延长线上时，如图所示：
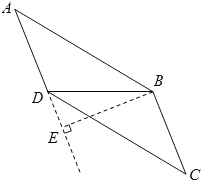
∵BE是AD边上的高，∠EBD=28°，
∴∠BDE=62°，
∵AD=BD，
∴∠A=∠ABD=
∠BDE=×62°=31°.
综上可知，∠A的度数为59° 或31°.
故答案为：59° 或31°.
练习册系列答案
名校课堂系列答案
相关题目
