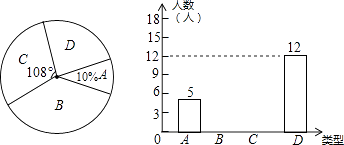
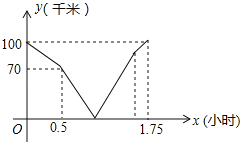
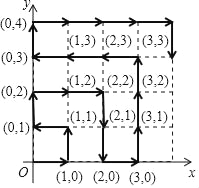
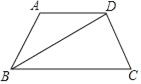
��Ŀ����
����Ŀ���Ķ�����
��̽���뷢�֣�
��һ����ѧ̽����У���ѧ��ȤС��ͨ��̽�����ֿ���ͨ�����������IJ�������ʾ�������������ľ�������ͼ1�������߶εij��ȿɱ�ʾΪ��AB=4-2=2��CB=4-(-2)=6��DC=-2-(-4)=2�������ۣ����������������ʾ����Ϊ�ֱ�a��b(b��a)�������������ľ���Ϊb-a(�����ýϴ������ȥ��С����)

�����������ã�
(1)��ͼ2��������E��F�����ʾ�����ֱ�Ϊ-2��-5���Լ��㣺EF=______��AF=______��
(2)�������Ϸֱ���������M��N��H����������M��ʾ����Ϊ-18����N��ʾ����Ϊ2018����֪��HΪ�߶�MN�е㣬����H��ʾ����m���������m��ֵ��
����չ�����죩
(3)��ͼ3����A��ʾ��x����B��ʾ-1����C��ʾ3x+8����AB=![]() BC�����A�͵�C�ֱ��ʾʲô����
BC�����A�͵�C�ֱ��ʾʲô����
(4)��(3)�����£���ͼ3���������Ƿ�������������ĵ�D��ʹDA+DC=3DB�������ڣ���ֱ��д����D��ʾ�������������ڣ���˵�����ɣ�
���𰸡�(1)3�� 7��(2)m=1000��(3)��A��ʾ��-2����C��ʾ������2��(4)��D����ʾ������-3��-![]() .
.
��������
��1�����õó��Ľ���ֱ�Ӽ��㼴�ɣ�
��2�����öԳƵ������з��̽�ɣ�
��3������ͼ��ʾ����������BC=4AB������������ô𰸣�
��4�������D��ʾ���������������г�����̽�ֵó��𰸼��ɣ�
(1)EF=-2-(-5)=3��FA=2-(-5)=7��
(2)m-(-18)=2018-m��
���m=1000��
(3)![]()
��ã�x=-2��
3x+8=2��
��A��ʾ��-2����C��ʾ������2��
(4)���ڣ����D��ʾ����Ϊd����������ã�-2-d+2-d=3(-1-d)���d=-3��
��d+2+2-d=3(d+1)�����![]() �ʵ�D����ʾ������-3��
�ʵ�D����ʾ������-3��![]() ��
��
�ʵ�D����ʾ������-3��![]() ��
��

 ��1����Ԫ�¿�������ĩϵ�д�
��1����Ԫ�¿�������ĩϵ�д�