题目内容
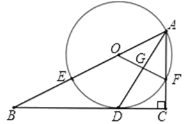
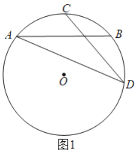
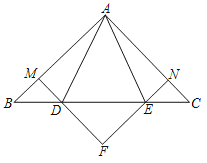
【题目】如图,等腰直角三角形ABC,∠BAC=90°,D、E是BC上的两点,且BD=CE,过D、E作DM、EN分别垂直AB、AC,垂足为M、N,交与点F,连接AD、AE.其中①四边形AMFN是正方形;②△ABE≌△ACD;③CE2+BD2=DE2;④当∠DAE=45°时,AD2=DECD.正确结论有( )
A.1个B.2个C.3个D.4个
【答案】C
【解析】
由三个角是直角的四边形是矩形,先判定四边形AMFN是矩形,再证明AM=AN,从而可判断①;利用SAS可判定△ABE≌△ACD,从而可判断②;在没有∠DAE=45°时,无法证得DE′=DE,故可判断③;由∠DAE=∠C,∠ADE=∠CDA可判定△ADE∽△CDA,从而可判定④.
解:∵DM、EN分别垂直AB、AC,垂足为M、N,
∴∠AMF=∠ANF=90°,
又∵∠BAC=90°,
∴四边形AMFN是矩形;
∵△ABC为等腰直角三角形,
∴AB=AC,∠ABC=∠C=45°,
∵DM⊥AB,EN⊥AC,
∴△BDM和△CEN均为等腰直角三角形,
又∵BD=CE,
∴△BDM≌△CEN(AAS),
∴BM=CN
∴AM=AN,
∴四边形AMFN是正方形,故①正确;
∵BD=CE,
∴BE=CD,
∵△ABC为等腰直角三角形,
∴∠ABC=∠C=45°,AB=AC,
∴△ABE≌△ACD(SAS),故②正确;
如图所示,将△ACE绕点A顺时针旋转90°至△ABE′,则CE=BE′,∠E′BA=∠C=45°,
由于△BDM≌△CEN,故点N落在点M处,连接ME′,则D、M、E′共线,
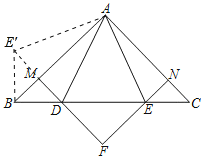
∵∠E′BA=45°,∠ABC=45°,
∴∠DBE′=90°,
∴BE′2+BD2=DE′2,
∴CE2+BD2=DE′2,
当∠DAE=45°时,∠DAE′=∠DAM+∠EAN=90°﹣45°=45°,
AE=AE′,AD=AD,
∴△ADE≌△ADE′(SAS),
∴DE′=DE,
∴在没有∠DAE=45°时,无法证得DE′=DE,故③错误;
∵AB=AC,∠ABD=∠C,BD=CE,
∴△ABD≌△ACE(SAS),
∴AD=AE,
∴当∠DAE=45°时,∠ADE=∠AED=67.5°,
∵∠C=45°,
∴∠DAE=∠C,∠ADE=∠CDA,
∴△ADE∽△CDA,
∴![]() =
=![]() ,
,
∴AD2=DECD,故④正确.
综上,正确的有①②④,共3个.
故选:C.

【题目】学校数学社团的同学们在学生中开展“了解校训意义”的调查活动.采取随机抽样的方式进行问卷调查.问卷调查的结果分为![]() 、
、![]() 、
、![]() 、
、![]() 四类.
四类.![]() 类表示非常了解;
类表示非常了解;![]() 类表示比较了解;
类表示比较了解;![]() 类表示基本了解;
类表示基本了解;![]() 类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类表示不太了解.(要求每位同学必须选并且只能选择一项)统计数据整理如表:
类别 | 频数 | 频率 |
| 20 |
|
|
| 0.3 |
| 11 | 0.22 |
| 4 | 0.08 |

(1)表中![]() __________;
__________;![]() _________.
_________.
(2)根据表中数据,求出![]() 类同学数所对应的扇形圆心角为_________度.
类同学数所对应的扇形圆心角为_________度.
(3)根据调查结果,请你估计该校1500名学生中对校训“非常了解”的人数;
(4)学校在开展了解校训意义活动中,需要从![]() 类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)
类的甲、乙、丙、丁四名同学中随机选取2人参加展示活动,求恰好选中甲乙两人的概率?(请用列表法或是树状图表示)