题目内容
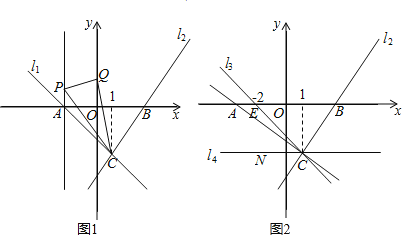
【题目】长江汛期即将来临，防汛指挥部在一危险地带两岸各安置了一探照灯，便于夜间查看江水及两岸河堤的情况．如图，灯A射线自AM顺时针旋转至AN便立即回转，灯B射线自BP顺时针旋转至BQ便立即回转，两灯不停交叉照射巡视．若灯A转动的速度是a度/秒，灯B转动的速度是b度/秒，且a，b满足|a﹣3b﹣1|+（a+b﹣5）2＝0．假定这一带长江两岸河堤是平行的，即PQ∥MN，且∠BAN＝45°．
（1）求a，b的值；
（2）若两灯同时转动，经过42秒，两灯射出的光束交于C，求此时∠ACB的度数；
（3）若灯B射线先转动10秒，灯A射线才开始转动，在灯B射线到达BQ之前，A灯转动几秒，两灯的光束互相平行？（直接写出答案）
【答案】（1）a＝4，b＝1；（2）∠ACB＝54°；（3）t＝
或 t＝70 或t＝
或t＝142；
【解析】
（1）根据|a﹣3b﹣1|+（a+b﹣5）2＝0，可得a﹣3b﹣1＝0，且a+b﹣4＝0 ,进而求出a,b的值
（2）根据题意两灯同时转动42秒可知∠PBC＝42°，∠MAC＝168°，再根据平行线的性质即可解答
（3）设A灯转动t秒，两灯的光束互相平行根据题意可知一共有四种情况①当0＜t＜45时②当45＜t＜90时③当90＜t＜135时④当135＜t＜170时，再把其代入到公式计算即可
（1）∵a、b满足|a﹣3b﹣1|+（a+b﹣5）2＝0，
∴a﹣3b﹣1＝0，且a+b﹣4＝0，
∴a＝4，b＝1；
（2）同时转动，t＝42时，
∠PBC＝42°，∠MAC＝168°，
∵PQ∥MN，
∴∠ACB＝54°，
（3）①当0＜t＜45时，
∴4t＝10+7，
解得t＝ ；
②当45＜t＜90时，
∴360﹣4t＝10+t，
解得t＝70；
③当90＜t＜135时，
∴4t﹣360＝10+t，
解得t＝ ；
④当135＜t＜170时，
∴720﹣4t＝10+t，
解得t＝142；
综上所述：t＝或 t＝70 或t＝或t＝142；
