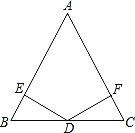
题目内容
【题目】阅读材料:如图(一),△ABC的周长为![]() ,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积
,内切圆O的半径为r,连结OA、OB、OC,△ABC被划分为三个小三角形,用S△ABC表示△ABC的面积
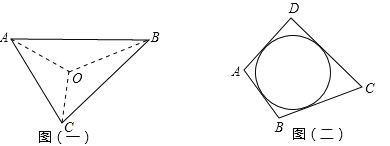
∵ S△ABC=S△OAB+S△OBC+S△OCA
又∵S△OAB=![]() ,S△OBC=
,S△OBC=![]() ,S△OCA =
,S△OCA =![]()
∴S△ABC=![]() +
+![]() +
+![]() =
=![]() (可作为三角形内切圆半径公式)
(可作为三角形内切圆半径公式)
(1)理解与应用:利用公式计算边长分为5、12、13的三角形内切圆半径;
(2)类比与推理:若四边形ABCD存在内切圆(与各边都相切的圆,如图(二))且面积为S,各边长分别为a、b、c、d,试推导四边形的内切圆半径公式;
(3)拓展与延伸:若一个n边形(n为不小于3的整数)存在内切圆,且面积为S,各边长分别为a1、a2、a3、…、an,合理猜想其内切圆半径公式(不需说明理由).
【答案】(1)2;(2)r=![]() ;(3)r=
;(3)r=![]() .
.
【解析】
试题分析:(1)根据上述三角形的内切圆的半径公式,由已知条件,结合勾股定理的逆定理得该三角形是直角三角形.可以首先求得其面积是30,其周长是5+12+13=30.再根据其公式代入计算;
(2)同样连接圆心和四边形的各个顶点以及圆心和的切点,根据四边形的面积等于四个直角三角形的面积进行计算;
(3)根据上述方法和结论,即可猜想到:任意多边形的内切圆的半径等于其面积的2倍除以多边形的周长.
试题解析:(1)以5,12,13为边长的三角形为直角三角形,易求得r=![]()
(2)连接OA,OB,OC,OD,并设内接圆半径为r,
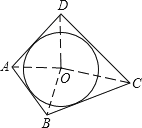
可得S四边形ABCD=S△OAB+S△OBC+S△OCD+S△ODA
=![]() a
a![]() r+
r+![]() b
b![]() r+
r+![]() c
c![]() r+
r+![]() d
d![]() r=
r=![]() (a+b+c+d)
(a+b+c+d)![]() r.
r.
∴r=![]() ;
;
(3)猜想:r=![]() .
.

练习册系列答案
相关题目