��Ŀ����
����Ŀ����1�����ⷢ��
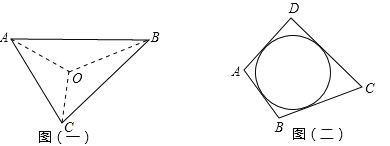
��ͼ1����ACB����DCE��Ϊ�ȱ������Σ���A��D��E��ͬһֱ���ϣ�����BE��
��գ��١�AEB�Ķ���Ϊ �����߶�AD��BE֮���������ϵΪ ��
��2����չ̽��
��ͼ2����ACB����DCE��Ϊ����ֱ�������Σ���ACB=��DCE=90������A��D��E��ͬһֱ���ϣ�CMΪ��DCE��DE���ϵĸߣ�����BE�����ж���AEB�Ķ������߶�CM��AE��BE֮���������ϵ����˵�����ɣ�

���𰸡�(1)��60������ȣ�(2)��2cm
��������
���������(1)�����ݵȱ������ε������Լ�������ȫ�ȵ����ʵó��𰸣�(2)��������ACD�ա�CEB�ó���CEB=��ADC=135��������AEB=135��-45��=90����Ȼ����ݵ���ֱ�������ε����ʵó���.
���������(1)��60�� ���
(2)���ߡ�ACD�ա�CEB ���CEB=��ADC=135�� ���AEB=135��-45��=90��
�ߡ�ACD�ա�CEB ��AD=BE �ڵ���ֱ��������CDE��CM=![]()
��AE-AD=DE ��AE-BE=2cm

 ��������ϵ�д�
��������ϵ�д� ���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�
���ɶ���ܲ��¿�ֱͨ�߿�ϵ�д�����Ŀ���������б���Ķ�Ӧֵ���ж�ax2+bx+c=0 ��a��0��a��b��cΪ��������һ����x��ȡֵ��Χ��_____
x | 3.23 | 3.24 | 3.25 | 3.26 |
ax2+bx+c | ��0.06 | ��0.02 | 0.03 | 0.09 |