Question

【题目】如图，是的内接三角形，的角平分线交于点，交于点，过点作直线．

（1）判断直线与的位置关系，并说明理由；

（2）若在上取一点使，求证：是的平分线；

（3）在（2）的条件下，若，，求的长．

Answer 1

【答案】（1）直线与相切，理由详见解析；（2）详见解析；（3）

【解析】

（1）如图（见解析），先根据角平分线的定义、圆周角定理得出，再根据垂径定理得出，然后根据平行线的性质得出，最后根据圆的切线的判定即可得证；

（2）先根据等腰三角形的性质得出，再根据角的和差、三角形的外角性质可得，然后根据圆周角定理可得，从而可得，最后根据角平分线的定义即可得证；

（3）根据相似三角形的判定与性质得出，由此计算即可得．

（1）直线与相切，理由如下：

如图，连接

∵平分

∴

∴

∴半径

∵

∴

∴直线与相切；

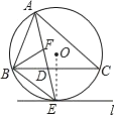
（2）∵

∴

∵，

∴

由圆周角定理得：

∴

∴是的平分线；

（3）∵，

∴

∴，即

解得．