题目内容
【题目】求证:三角形的一条中位线与第三边上的中线互相平分.
要求:(1)根据给出的![]() 和它的一条中位线
和它的一条中位线![]() ,在给出的图形上,请用尺规作出
,在给出的图形上,请用尺规作出![]() 边上的中线
边上的中线![]() ,交
,交![]() 于点
于点![]() .不写作法,保留痕迹;
.不写作法,保留痕迹;
(2)据此写出已知,求证和证明过程.

【答案】(1)作线段![]() 的中段线,
的中段线,![]() 的中点为
的中点为![]() ,连结
,连结![]() 即可,见解析;(2) 见解析.
即可,见解析;(2) 见解析.
【解析】
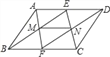
(1)作BC的垂直平分线得到BC的中点F,从而得到BC边上的中线AF;
(2)写出已知、求证,连接DF、EF,如图,先证明EF为AB边的中位线,利用三角形中位线性质得到EF∥AD,EF=AD,则可判断四边形ADFE为平行四边形,从而得到DE与AF互相平分.
解:(1)作线段![]() 的中段线,
的中段线,![]() 的中点为
的中点为![]() ,连结
,连结![]() 即可。
即可。
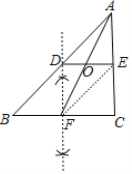
(2)已知:![]() 分别为
分别为![]() 三边
三边![]() 的中点,
的中点,![]() 与
与![]() 交于点
交于点![]() 。
。
求证:![]() 与
与![]() 互相平分。
互相平分。
证明:连结![]() ,
,
![]() 分别为
分别为![]() 的中点,
的中点,
有![]() ,
,
又![]() 为
为![]() 中点,
中点,
所以,![]() ,
,
四边形![]() 为平行四边形,
为平行四边形,
所以,![]() 与
与![]() 互相平分.
互相平分.

练习册系列答案
 夺冠金卷全能练考系列答案
夺冠金卷全能练考系列答案
相关题目
【题目】电话计费问题
下表中有两种移动电话计费方式方式
月使用费/元 | 主叫限定 时间/min | 主叫超时 费/(元/min) | 被叫 | |
方式一 | 50 | 120 | 0.2 | 免费 |
方式二 | 80 | 300 | 0.1 | 免费 |
解决问题:
(1)设一个月内使用移动电话主叫时间为t分钟(为正整数).根据上表信息填写下表:
主叫时间t(分钟) | 方式一计费(元) | 方式二计费(元) |
| 50 | 80 |
| ||
|
(2)如果王刚每月打电话的主叫时间t不超过500分钟,请你帮助他分析选择一种省钱的计费方式,并说明理由.