题目内容
【题目】如图,抛物线![]() 交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
交x轴于点A(-3,0)和点B,交y轴于点C(0,3).
(1)求抛物线的函数表达式;
(2)若点Q是线段AC上的一动点,作DQ⊥x轴,交抛物线于点D,求线段DQ长度的最大值.
(3)点G是抛物线上的动点,点F在x轴上的动点,若以A,C,F,G四个点为顶点的四边形是平行四边形,求出所有满足条件的点F坐标(直接写出结果).

【答案】(1)y=-x2-2x+3;(2)QD最大值为![]() ;(3)(-1,0),(-5,0),(
;(3)(-1,0),(-5,0),(![]() ,0),(
,0),(![]() ,0).
,0).
【解析】
(1)将点A、C的坐标代入抛物线解析式,利用待定系数法求二次函数解析式解答;
(2)利用待定系数法求一次函数解析式求出直线AC的解析式,然后表示出DQ,再根据二次函数的最值问题解答;
(3)设点![]() ,再分情况根据平行四边形的性质求出所有满足条件的点F坐标即可.
,再分情况根据平行四边形的性质求出所有满足条件的点F坐标即可.
将点![]() ,点
,点![]() 代入
代入![]() 得
得
![]()
解得![]()
∴抛物线的函数表达式为![]()
(2)设直线AC的解析式为![]()
则![]()
解得![]()
∴直线AC的解析式为![]() ,
,
![]()
![]()
![]()
![]()
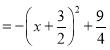
∴当![]() 时,线段DQ长度的最大值为
时,线段DQ长度的最大值为![]()
(3)设点![]() ,
,
①如图,
∵![]() ,点
,点![]() ,点
,点![]()
∴![]()
![]()
解得![]()
∴![]()
∴![]()
∴![]()
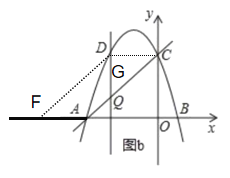
②如图,
∵![]() ,点
,点![]() ,点
,点![]()
∴![]()
![]()
解得![]()
∴![]()
∴![]()
∴![]()

③如图,
∵平行四边形对角线互相平分
∴点C和点G的纵坐标之和为0
∵点![]()
∴![]()
![]()
![]()
![]()
解得![]()
当![]() 时,对角线交点坐标为
时,对角线交点坐标为
∴![]()
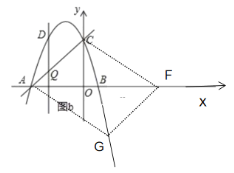
④如图,根据③可得
当![]() 时,对角线交点坐标为
时,对角线交点坐标为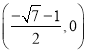
∴![]()
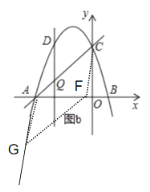
故所有满足条件的点F的坐标为(-1,0),(-5,0),(![]() ,0),(
,0),(![]() ,0).
,0).

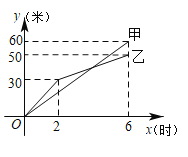
【题目】某校为了解八年级学生课外阅读情况,随机抽取20名学生平均每周用于课外阅读读的时间(单位:![]() ),过程如下:
),过程如下:
(收集数据)
30 | 60 | 81 | 50 | 40 | 110 | 130 | 146 | 90 | 100 |
60 | 81 | 120 | 140 | 70 | 81 | 10 | 20 | 100 | 81 |
(整理数据)
课外阅读时间 |
|
|
|
|
等级 |
|
|
|
|
人数 | 3 |
| 8 |
|
(分析数据)
平均数 | 中位数 | 众数 |
80 |
|
|
请根据以上提供的信息,解答下列问题:
(1)填空:![]() ______,
______,![]() ______,
______,![]() ______,
______,![]() ______;
______;
(2)如果每周用于课外读的时间不少于![]() 为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?
为达标,该校八年级现有学生200人,估计八年级达标的学生有多少人?