题目内容
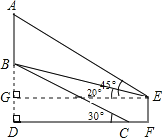
【题目】如图 1,在矩形 ABCD 中,点 E 以 lcm/s 的速度从点 A 向点 D 运动,运动时间为 t(s),连结 BE,过点 E 作 EF⊥BE,交 CD 于 F,以 EF 为直径作⊙O.
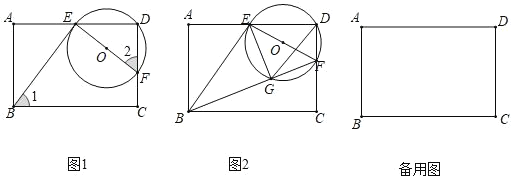
(1)求证:∠1=∠2;
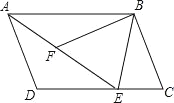
(2)如图 2,连结 BF,交⊙O 于点 G,并连结 EG.已知 AB=4,AD=6.
①用含 t 的代数式表示 DF 的长
②连结 DG,若△EGD 是以 EG 为腰的等腰三角形,求 t 的值;
(3)连结 OC,当 tan∠BFC=3 时,恰有 OC∥EG,请直接写出 tan∠ABE 的值.
【答案】(1)见解析;(2)①![]() ,②若△EGD 是以 EG 为腰的等腰三角形,t 的值为 3 或
,②若△EGD 是以 EG 为腰的等腰三角形,t 的值为 3 或![]() ;(3)tan∠ABE=1.
;(3)tan∠ABE=1.
【解析】
(1)根据矩形的性质得到AD∥BC,∠A=∠ADC=90°,根据余角的性质即可得到结论;
(2)①根据相似三角形的性质即可得到结论;
②当EG=ED时,根据相似三角形的性质得到结论;当GE=GD时,根据全等三角形的性质和勾股定理即可得到结论;
(3)如图2,过O作OH⊥CD于H,设CF=a,BC=3a,得到DE=3a-t,根据三角形的中位线的性质得到OH=![]() DE=
DE=![]() ,根据三角函数的定义得到DF=7a-3t,AB=8a-3t,根据相似三角形的性质即可得到结论.
,根据三角函数的定义得到DF=7a-3t,AB=8a-3t,根据相似三角形的性质即可得到结论.
(1)∵四边形 ABCD 是矩形,
∴AD∥BC,∠A=∠ADC=90°,
∴∠AEB=∠1,
∵EF⊥BE,
∴∠AEB+∠DEF=90°,
∵∠2+∠DEF=90°,
∴∠AEB=∠2,
∴∠1=∠2;
(2)①∵∠A=∠ADC=90°,∠AEB=∠EFD,
∴△ABE∽△DEF,
∴![]() ,
,
∵AB=4,AE=t,DE=6﹣t,
∴![]() ,
,
∴![]() ,
,
②当 EG=ED 时,
∴∠EGD=∠EDG,
∵∠EGD=∠EFD,∠EDG=∠EFG,
∴∠EFD=∠EFG=∠AEB,
∵∠A=∠EDF=∠BEF,
∴△BAE∽△EDF∽△BEF,
∴![]() =
=![]() =
=![]() ,
,
∴AE=DE,
∴t=6﹣t,
∴t=3;
当 GE=GD 时,∴∠GED=∠GDE,
∵∠EDG=∠BFE,∠GED=∠BFC,
∴∠BFE=∠BFC,
∵∠BEF=∠C=90°,BF=BF,
∴△BEF≌△BCF(AAS),
∴BE=BC=6,
∵AB2+AE2=BE2,
∴42+t2=62,
∴t=2![]() ;
;
综上所述,若△EGD 是以 EG 为腰的等腰三角形,t 的值为 3 或 ![]() ;
;
(3)tan∠ABE=1,
理由:如图 2,过 O 作 OH⊥CD 于 H,
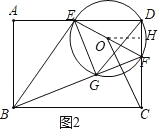
∵tan∠BFC=![]() =3,
=3,
设 CF=a,BC=3a,
∵AE=t,
∴DE=3a﹣t,
∵OH⊥CD,AD⊥CD,
∴OH∥DE,
∵OF=OE,
∴OH=![]() DE=
DE=![]() ,
,
∵OC∥EG,EG⊥FG,
∴OC⊥FG,
∴tan∠COH=tan∠BFC=3,
∴CH=3OH=![]() ,FH=
,FH=![]() ,
,
∴DF=7a﹣3t,AB=8a﹣3t,
由△ABE∽△DEF,得 ![]() ,
, ![]() ,
,
解得t1=2a,t2=![]() a,
a,
当t=![]() a时,8a-3t<0,不合题意,舍去;
a时,8a-3t<0,不合题意,舍去;
当t=2a时,
∴tan∠ABE=![]() =
=![]() =
=![]() =1.
=1.

 阅读快车系列答案
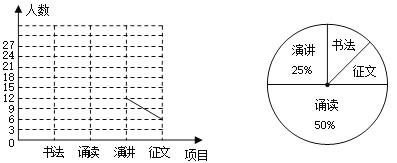
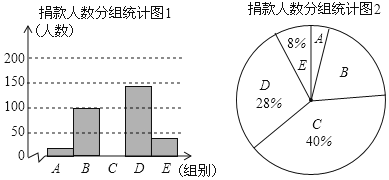
阅读快车系列答案【题目】我校“点爱”社团倡导全校学生参加“关注特殊儿童”自愿捐款活动,并对此次活动进行抽样调查,得到一组学生捐款情况的数据,将数据整理成如图所示的统计图(图中信息不完整).已知A、B两组捐款人数的比为1:5.请结合以上信息解答下列问题.
组别 | 捐款额x/元 | 人数 |
A | 1≤x<10 | |
B | 10≤x<20 | 100 |
C | 20≤x<30 | |
D | 30≤x<40 | |
E | x≥40 |
(1)a= ,本次抽样调查样本的容量是 ;
(2)补全“捐款人数分组统计图1”;
(3)若记A组捐款的平均数为5元,B组捐款的平均数为15元,C组捐款的平均数为25元,D组捐款的平均数为35元,E组捐款的平均数为50元,全校共有2000名学生参加此次活动,请你估计此次活动可以筹得善款的金额大约为多少元.