Question

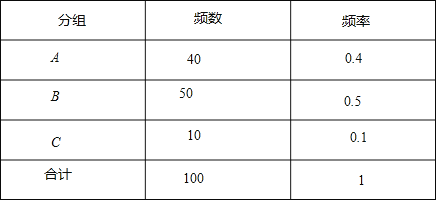
【题目】“数学运算”是数学学科核心素养之一，某校对七年级学生“数学运算能力”情况进行调研，从该校360名七年级学生中抽取了部分学生进行运算能力测试井进行分析，成绩分为A、B、C三个层次，绘制了频数分布表（如下），请根据图表信息解答下列问题：

（1）补全频数分布；

（2）如果成绩为A等级的同学属于优秀，请你估计该校七年级约有多少人达到优秀水平？

Answer 1

【答案】（1）总人数为100人，B层次的人数50，A层次的频率为0.4；（2）约有144人达到优秀水平．

【解析】

（1）先利用C层次的频数除以它所占的频率得到调查的总人数，然后计算出A层次的频率、B层次的频数后补全频数分布表；

（2）用360乘以样本中A层次的频率可估计出该校七年级达到优秀水平的人数．

解：（1）10÷0.1＝100，

调查的总人数为100人，

所以B层次的人数为100﹣40﹣10＝50，

A层次的频率为40÷100＝0.4；

（2）360×0.4＝144，

所以估计该校七年级约有144人达到优秀水平．