题目内容
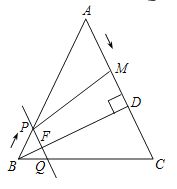
【题目】如图,在Rt△ABC中,∠ACB=90°,AB=5,过点B作BD⊥AB,点C,D都在AB上方,AD交△BCD的外接圆⊙O于点E.
(1)求证:∠CAB=∠AEC.
(2)若BC=3.
①EC∥BD,求AE的长.
②若△BDC为直角三角形,求所有满足条件的BD的长.
(3)若BC=EC=![]()
![]() ,则
,则![]() = .(直接写出结果即可)
= .(直接写出结果即可)

【答案】(1)见解析;(2)①AE=![]() ,②BD=
,②BD=![]()
![]() ;(3)
;(3)![]() .
.
【解析】
(1)利用圆的内接四边形的性质以及等角的余角相等的性质易证明出结论成立;
(2)延长AC交BD于点F,利用平行线等分线段和相似三角形对应边成比例求解即可;
(3)利用勾股定理和相似三角形分别求出AE和BD的长,依据对应边等高三角形的面积比是对应边之比,进而求解;

证明:(1)∵四边形BCED内接于⊙O
∴∠AEC=∠DBC
又∵DB⊥AB
∴∠ABC+∠DBC=90°
又∵∠ACB=90°
∴在Rt△ABC中,∠CAB+∠ABC=90°
∴∠DBC=∠CAB
∴∠CAB=∠AEC
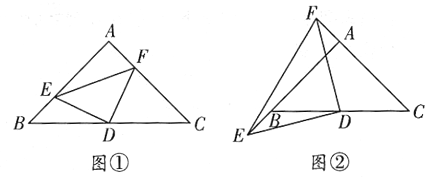
(2)①如图1延长AC交BD于点F,延长EC交AB于点G.
∵在Rt△ABC中,AB=5,BC=3
∴由勾股定理得,AC=4
又∵BC⊥AF,AB⊥BF
∠AFB=∠BFC
∴Rt△AFB∽Rt△BFC
∴![]()
∴BC2=CFAC
即9=CF4,解得,CF=![]()
又∵EC∥BD
∴CG⊥AB
∴ABCG=ACBC
即5CG=4×3,解得,CG=![]()
又∵在Rt△ACG中,AG=![]() =
=![]()
又∵EC∥DB
∴∠AEC=∠ADB
由(1)得,∠CAB=∠AEC
∴∠ADB=∠CAB
又∵∠ACB=∠DBA=90°
∴Rt△ABC∽Rt△DBA
∴![]()
得AD=![]()
又∵EG∥BD
∴![]()
得AE=![]()
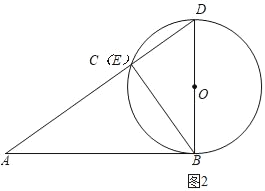
②当△BDC是直角三角形时,如图二所示
∵∠BCD=90°
∴BD为⊙O直径
又∵∠ACB=90°
∴A、C、D三点共线
即BC⊥AD时垂足为C,此时C点与E点重合.
又∵∠DAB=∠BAC,∠ACB=ABD=90°
∴Rt△ACB∽Rt△ABD
∴![]()
得AD=![]()
又∵在Rt△ABD中,BD=![]()
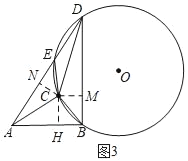
③如图三,由B、C、E都在⊙O上,且BC=CE=![]()
∴![]()
∴∠ADC=∠BDC
即DC平分∠ADB
过C作CM⊥BD,CN⊥AD,CH⊥AB垂足分别为M、N.,H.
∵在Rt△ACB中AB=5,BC=![]()
∴AC=2![]()
又∵在Rt△ACB中CH⊥AB
∴ABCH=ACBC
即5CH=2![]() ×
×![]()
解得,CH=2
∴MB=2
又∵DC平分∠ADB
∴CM=CN
又∵在Rt△CHB中BC=5,CH=2
∴HB=1
∴CM=CN=1
又∵在△DCN与△DCM中

∴△DCN与△DCM(AAS)
∴DN=DM
设DN=DM=x
则BD=x+2,AD=x+![]()
在Rt△ABD中由AB2+BD2=AD2得,
25+(x+2)2=(x+![]() )2
)2
解得,x=![]()
∴BD=BM+MD=2+![]() =
=![]()
又由(1)得∠CAB=∠AEC,且∠ENC=∠ACB
∴△ENC∽△ACB
∴![]()
∴NE=2
又∵在Rt△CAN中CN=1,AC=2![]()
∴AN=![]() =
=![]()
∴AE=AN+NE=![]() +2
+2
又∵S△BCD=![]() BDCM,S△ACE=
BDCM,S△ACE=![]() AECN,CM=CN
AECN,CM=CN
∴![]()
故![]()
![]() .
.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案