题目内容
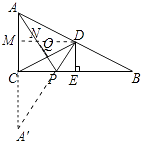
【题目】如图，在Rt△ABC中，∠ACB=90°，点D是AB边的中点，过D作DE⊥BC于点E，点P是边BC上的一个动点，AP与CD相交于点Q．当AP+PD的值最小时，AQ与PQ之间的数量关系是（ ）
A.AQ= 
PQ
B.AQ=3PQ
C.AQ= 
PQ
D.AQ=4PQ
【答案】B
【解析】如图，作点A关于BC的对称点A′，连接A′D交BC于点P，此时PA+PD最小．作DM∥BC交AC于M，交PA于N．
∵∠ACB=∠DEB=90°，
∴DE∥AC，
∵AD=DB，
∴CE=EB，
∴DE= 
AC= CA′，
∵DE∥CA′，
∴ 
= 
= ，
∵DM∥BC，AD=DB，
∴AM=MC，AN=NP，
∴DM= BC=CE=EB，MN= PC，
∴MN=PE，ND=PC，
在△DNQ和△CPQ中，
，
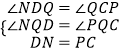∴△DNQ≌△CPQ，
∴NQ=PQ，
∵AN=NP，
∴AQ=3PQ．
所以答案是：B．
【考点精析】掌握轴对称-最短路线问题是解答本题的根本，需要知道已知起点结点，求最短路径；与确定起点相反，已知终点结点，求最短路径；已知起点和终点，求两结点之间的最短路径；求图中所有最短路径．
练习册系列答案
名校课堂系列答案
相关题目
【题目】永州市是一个降水丰富的地区，今年4月初，某地连续降雨导致该地某水库水位持续上涨，下表是该水库4月1日～4月4日的水位变化情况：
日期x | 1 | 2 | 3 | 4 |
水位y（米） | 20.00 | 20.50 | 21.00 | 21.50 |
（1）请建立该水库水位y与日期x之间的函数模型；
（2）请用求出的函数表达式预测该水库今年4月6日的水位；
（3）你能用求出的函数表达式预测该水库今年12月1日的水位吗？
