Question

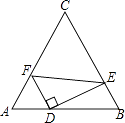
【题目】如图，点O为平面直角坐标系的原点，点A在x轴上，△AOC是边长为2的等边三角形．

（1）写出△AOC的顶点C的坐标：_____．

（2）将△AOC沿x轴向右平移得到△OBD，则平移的距离是_____

（3）将△AOC绕原点O顺时针旋转得到△OBD，则旋转角可以是_____度

（4）连接AD，交OC于点E，求∠AEO的度数．

Answer 1

【答案】（1）（﹣1，）；（2）2；（3）120；（4）∠AEO=90°．

【解析】

（1）过C作CH⊥AO于H，则HO=1，根据勾股定理可得，则可求点C坐标；（2）根据平移的性质可得△AOC沿x轴向右平移2个单位得到△OBD；（3）由等边三角形的性质和旋转可得，旋转角=∠AOD=120°；（4）根据平移的性质可得AC∥OD，进而可证△ACE≌△DOE，则CE=OE，根据等边三角形的性质得结论

（1）如图，过C作CH⊥AO于H，则HO=AO=1，

∴Rt△COH中，，

∴点C的坐标为，

故答案为：；

（2）由平移可得，平移的距离=AO=2，

故答案为：2；

（3）由旋转可得，旋转角=∠AOD=120°，

故答案为：120；

（4）如图，∵AC∥OD，

∴∠CAE=∠ODE，∠ACE=∠DOE，

又∵AC=DO，

∴△ACE≌△DOE，

∴CE=OE，

∴AD⊥CO，即∠AEO=90°．