题目内容
【题目】已知，△ABC是边长3cm的等边三角形．动点P以1cm/s的速度从点A出发，沿线段AB向点B运动．
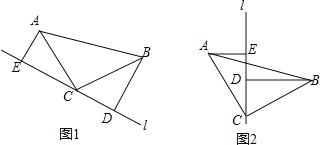
（1）如图1，设点P的运动时间为t（s），那么t＝ （s）时，△PBC是直角三角形；
（2）如图2，若另一动点Q从点B出发，沿线段BC向点C运动，如果动点P、Q都以1cm/s的速度同时出发．设运动时间为t（s），那么t为何值时，△PBQ是直角三角形？
（3）如图3，若另一动点Q从点C出发，沿射线BC方向运动．连接PQ交AC于D．如果动点P、Q都以1cm/s的速度同时出发．设运动时间为t（s），那么t为何值时，△DCQ是等腰三角形？
（4）如图4，若另一动点Q从点C出发，沿射线BC方向运动．连接PQ交AC于D，连接PC．如果动点P、Q都以1cm/s的速度同时出发．请你猜想：在点P、Q的运动过程中，△PCD和△QCD的面积有什么关系？并说明理由．
【答案】（1）
；（2）t＝1或2（s）；（3）t＝1（s）；（4）面积相等，理由见解析
【解析】
（1）当△PBC是直角三角形时，∠B＝60°，所以BP＝1.5cm，即可算出t的值；
（2）因为∠B＝60°，可选取∠BPQ＝90°或∠BQP＝90°，然后根据勾股定理计算出BP长，即可算出t的大小；
（3）因为∠DCQ＝120°，当△DCQ是等腰三角形时，CD＝CQ，然后可证明△APD是直角三角形，即可根据题意求出t的值；
（4）面积相等．可通过同底等高验证．
解：（1）当△PBC是直角三角形时，∠B＝60°，
∠BPC＝90°，所以BP＝1.5cm，
所以t＝.
（2）当∠BPQ＝90°时，BP＝0.5BQ，
3﹣t＝0.5t，所以t＝2；
当∠BQP＝90°时，BP＝2BQ，
3﹣t＝2t，所以t＝1；
所以t＝1或2（s）;
（3）因为∠DCQ＝120°，当△DCQ是等腰三角形时，CD＝CQ，
所以∠PDA＝∠CDQ＝∠CQD＝30°，
又因为∠A＝60°，
所以AD＝2AP，2t+t＝3，
解得t＝1（s）；
（4）相等，如图所示：
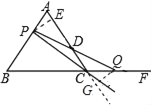
作PE⊥AD于E，QG⊥AD延长线于G，则PE∥QG，则易知∠G＝∠AEP，∠A＝∠ACB＝∠QCG＝60°，
在△EAP和△GCQ中，
因为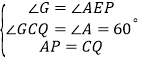
，
所以△EAP≌△GCQ（AAS），
所以PE＝QG，所以，△PCD和△QCD同底等高，所以面积相等．
