题目内容
【题目】如图,已知四边形ABCD是矩形,把矩形沿直线AC折叠,点B落在点E处,连接DE.若DE:AC=3:5,则 ![]() 的值为 .
的值为 . 
【答案】![]()
【解析】解:∵矩形沿直线AC折叠,点B落在点E处,
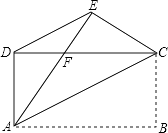
∴∠BAC=∠EAC,AE=AB=CD,
∵矩形ABCD的对边AB∥CD,
∴∠DCA=∠BAC,
∴∠EAC=∠DCA,
设AE与CD相交于F,则AF=CF,
∴AE﹣AF=CD﹣CF,
即DF=EF,
∴ ![]() =
= ![]() ,
,
又∵∠AFC=∠EFD,
∴△ACF∽△EDF,
∴ ![]() =
= ![]() =
= ![]() ,
,
设DF=3x,FC=5x,则AF=5x,
在Rt△ADF中,AD= ![]() =
= ![]() =4x,
=4x,
又∵AB=CD=DF+FC=3x+5x=8x,
∴ ![]() =
= ![]() =
= ![]() .
.
故答案为: ![]() .
.
根据翻折的性质可得∠BAC=∠EAC,再根据矩形的对边平行可得AB∥CD,根据两直线平行,内错角相等可得∠DAC=∠BCA,从而得到∠EAC=∠DAC,设AE与CD相交于F,根据等角对等边的性质可得AF=CF,再求出DF=EF,从而得到△ACF和△EDF相似,根据相似三角形对应边成比例
设DF=3x,FC=5x,在Rt△ADF中,利用勾股定理列式求出AD,再根据矩形的对边相等求出AB,然后代入进行计算即可得到所求的值.

练习册系列答案
 阅读快车系列答案
阅读快车系列答案
相关题目