Question

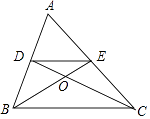
【题目】如图，CD⊥AB于D，点E为AC上一动点，过点E作EF⊥AB于F，连接DE．

（1）若∠1＝∠2，求证：DE∥BC；

（2）在点E运动过程中，直线DE与直线BC交于点M，若∠DCB＝α，∠M＝β，则∠FED的度为　 （用含α，β的式子表示）．

Answer 1

【答案】（1）见解析；（2）α+β或α﹣β．

【解析】

（1）根据CD⊥AB，EF⊥AB，可以得到CD∥EF，然后根据平行线的性质，可以得到∠1和∠3的关系，从而可以得到∠2和∠3的关系，进而可以得到结论成立；

（2）根据题意可以画出相应的图形，从而可以用α和β表示出∠FED的度数．

（1）如图1所示，

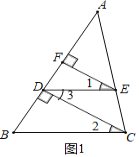
∵CD⊥AB，EF⊥AB，

∴CD∥EF，

∴∠1＝∠3，

又∵∠1＝∠2，

∴∠2＝∠3，

∴DE∥BC；

（2）如图2所示，

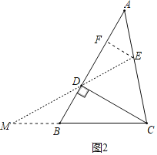
∵∠DCB＝α，∠M＝β，

∴∠EDC＝∠DCB+∠M＝α+β；

如图3所示，

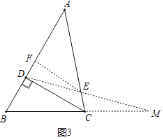
∵∠DCB＝α，∠M＝β，

∴∠DCB＝∠EDC+∠M

∴∠EDC＝α﹣β；

由上可得，

故答案为：α+β或α﹣β．