题目内容
【题目】如图,在△ABC中,两条中线BE、CD相交于点O,则S△ADE:S△COE= . 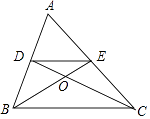
【答案】2:1
【解析】解:∵在△ABC中,两条中线BE、CD相交于点O,
∴DE为中位线,
∴DE∥BC,DE= ![]() BC,
BC,
∴△ADE∽△ABC,△DOE∽△COB,
∴S△ADE:S△ABC=1:4,S△DOE:S△COB=1:4,
∵OD:OC=1:2,
∴S△DOE:S△COE=1:2,S△DOB:S△COB=1:2,
∴S△COE= ![]() S四边形DBCE,
S四边形DBCE,
则S△ADE:S△COE=2:1.
所以答案是:2:1
【考点精析】解答此题的关键在于理解三角形中位线定理的相关知识,掌握连接三角形两边中点的线段叫做三角形的中位线;三角形中位线定理:三角形的中位线平行于三角形的第三边,且等于第三边的一半,以及对相似三角形的判定与性质的理解,了解相似三角形的一切对应线段(对应高、对应中线、对应角平分线、外接圆半径、内切圆半径等)的比等于相似比;相似三角形周长的比等于相似比;相似三角形面积的比等于相似比的平方.

练习册系列答案
相关题目