题目内容
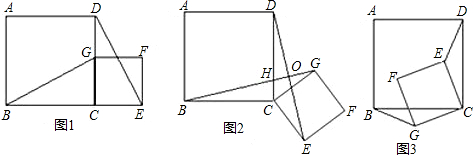
如图1,四边形ABCD是正方形,G是CD边上的一个动点(点G与C、D不重合),以CG为一边在正方形ABCD外作正方形CEFG,连接BG,DE.我们探究下列图中线段BG、线段DE的长度关系及所在直线的位置关系:(1)①猜想如图1中线段BG、线段DE的长度关系及所在直线的位置关系;
②将图1中的正方形CEFG绕着点C按顺时针(或逆时针)方向旋转任意角度α,得到如图2,如图3情形.请你通过观察、测量等方法判断①中得到的结论是否仍然成立,并选取图2证明你的判断;
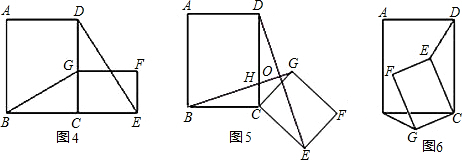
(2)将原题中正方形改为矩形(如图4-6),且AB=a,BC=b,CE=ka,CG=kb(a≠b,k>0),第(1)题①中得到的结论哪些成立,哪些不成立?若成立,以图5为例简要说明理由;
(3)在第(2)题图5中,连接DG、BE,且a=3,b=2,k=
| 1 | 2 |
分析:(1)四边形ABCD是正方形推出△BCG≌△DCE.然后得出∠DOH=90°,推出BG⊥DE.
(2)依题意得出AB=a,BC=b,CG=kb,CE=ka的线段比例,然后再推出∠CDE+∠DHO=90°即可.
(3)依题意得出BE2+DG2=BD2+GE2,从而可求解.
(2)依题意得出AB=a,BC=b,CG=kb,CE=ka的线段比例,然后再推出∠CDE+∠DHO=90°即可.
(3)依题意得出BE2+DG2=BD2+GE2,从而可求解.
解答:解:(1)①BG=DE,
BG⊥DE.
②BG=DE,
BG⊥DE仍然成立.
在图(2)中证明如下
∵四边形ABCD、四边形CEFG都是正方形,
∴BC=CD,CG=CE,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE(1分),
∵在△BCG与△DCE中,
,
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE.
(2)BG⊥DE成立,BG=DE不成立.
简要说明如下:
∵四边形ABCD、四边形CEFG都是矩形,
且AB=a,BC=b,CG=kb,CE=ka(a≠b,k>0),
∴
=
=
,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE,
∴△BCG∽△DCE,
∴∠CBG=∠CDE,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE.
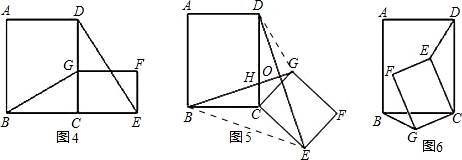
(3)∵BG⊥DE,
∴OB2+OD2=BD2,OE2+OG2=GE2,OB2+OE2=BE2,OG2+OD2=DG2,
∴BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2,
又∵a=3,b=2,k=
,
∴BD2+GE2=22+32+12+(
)2=
,
∴BE2+DG2=
.
BG⊥DE.
②BG=DE,
BG⊥DE仍然成立.
在图(2)中证明如下
∵四边形ABCD、四边形CEFG都是正方形,
∴BC=CD,CG=CE,∠BCD=∠ECG=90°,
∴∠BCG=∠DCE(1分),
∵在△BCG与△DCE中,
|
∴△BCG≌△DCE(SAS),
∴BG=DE,∠CBG=∠CDE,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE.
(2)BG⊥DE成立,BG=DE不成立.
简要说明如下:
∵四边形ABCD、四边形CEFG都是矩形,
且AB=a,BC=b,CG=kb,CE=ka(a≠b,k>0),
∴
| BC |
| DC |
| CG |
| CE |
| b |
| a |
∴∠BCG=∠DCE,
∴△BCG∽△DCE,
∴∠CBG=∠CDE,
又∵∠BHC=∠DHO,∠CBG+∠BHC=90°,
∴∠CDE+∠DHO=90°,
∴∠DOH=90°,
∴BG⊥DE.

(3)∵BG⊥DE,
∴OB2+OD2=BD2,OE2+OG2=GE2,OB2+OE2=BE2,OG2+OD2=DG2,
∴BE2+DG2=OB2+OE2+OG2+OD2=BD2+GE2,
又∵a=3,b=2,k=
| 1 |
| 2 |
∴BD2+GE2=22+32+12+(
| 3 |
| 2 |
| 65 |
| 4 |
∴BE2+DG2=
| 65 |
| 4 |
点评:解答本题要充分利用正方形的特殊性质.注意在正方形中的特殊三角形的应用,搞清楚矩形、菱形、正方形中的三角形的三边关系,利用勾股定理求解,可有助于提高解题速度和准确率.

练习册系列答案
相关题目
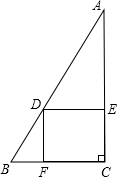 足分别为E、F,得四边形DECF,设DE=x,DF=y.
足分别为E、F,得四边形DECF,设DE=x,DF=y. 如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( )
如图,AD是△ABC的中线,AE=EF=FC,BE、AD相交于点G,下列4个结论:①DF∥GE;②DF:BG=2:3;③AG=GD;④S△BGD=S四边形EFDG;其中正确的有( ) 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD. 已知:如图,在四边形ABC中,AD=BC,AB=CD.
已知:如图,在四边形ABC中,AD=BC,AB=CD.