题目内容
【题目】一个不透明的口袋中有四个完全相同的小球,把它们分别标号为1,2,3,4.随机摸取一个小球然后放回,再随机摸出一个小球,请用树状图或列表法求下列事件的概率.
(1)两次取出的小球的标号相同;
(2)两次取出的小球标号的和等于6.
【答案】(1)![]() ;(2)
;(2)![]() =
=![]() .
.
【解析】
列出列表法就出来了,第一问只需找到相同小球的种类数比上所有可能就出来了,
第二问找到小球和等于6的所有种类数比上所有可能就出来了
解:
1 | 2 | 3 | 4 | |
1 | (1,1) | (2,1) | (3,1) | (4,1) |
2 | (1,2) | (2,2) | (3,2) | (4,2) |
3 | (1,3) | (2,3) | (3,3) | (4,3) |
4 | (1,4) | (2,4) | (3,4) | (4,4) |
(1) 设两次取出小球的标号相同的概率为P,总共有16种可能,其中4种两次取的小球标号一样,∴P=![]()
(2) 设两次取出的小球的和等于6的概率为![]() ,有三种情况,2+4=6,3+3=6,4+2=6
,有三种情况,2+4=6,3+3=6,4+2=6
∴![]() =
=![]()

练习册系列答案
 学练快车道口算心算速算天天练系列答案
学练快车道口算心算速算天天练系列答案
相关题目
【题目】某市将实行居民生活用电阶梯电价方案,如下表,图中折线反映了每户居民每月电费![]() (元)与用电量
(元)与用电量![]() (度)间的函数关系.
(度)间的函数关系.
档次 | 第一档 | 第二档 | 第三档 |
每月用电量 |
|
|
|
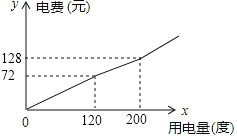
(1)小王家某月用电![]() 度,需交电费___________元;
度,需交电费___________元;
(2)求第二档电费![]() (元)与用电量
(元)与用电量![]() (度)之间的函数关系式;
(度)之间的函数关系式;
(3)小王家某月用电![]() 度,交纳电费
度,交纳电费![]() 元,请你求出第三档每度电费比第二档每度电费多多少元?
元,请你求出第三档每度电费比第二档每度电费多多少元?