题目内容
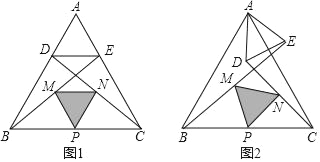
【题目】如图1,在等边△ABC中,点D,E分别在边AB,AC上,AD=AE,连接BE,CD,点M、N、P分别是BE、CD、BC的中点.
(1)观察猜想:图1中,△PMN的形状是 ;
(2)探究证明:把△ADE绕点A逆时针方向旋转到图2的位置,△PMN的形状是否发生改变?并说明理由;
(3)拓展延伸:把△ADE绕点A在平面内自由旋转,若AD=1,AB=3,请直接写出△PMN的周长的最大值.
【答案】(1) 等边三角形;(2) △PMN的形状不发生改变,仍然为等边三角形,理由见解析;(3)6
【解析】分析:(1)如图1,先根据等边三角形的性质得到AB=AC,∠ABC=∠ACB=60°,则BD=CE,再根据三角形中位线性质得PM∥CE,PM=![]() CE,PN∥AD,PN=
CE,PN∥AD,PN=![]() BD,从而得到PM=PN,∠MPN=60°,从而可判断△PMN为等边三角形;
BD,从而得到PM=PN,∠MPN=60°,从而可判断△PMN为等边三角形;
(2)连接CE、BD,如图2,先利用旋转的定义,把△ABD绕点A逆时针旋转60°可得到△CAE,则BD=CE,∠ABD=∠ACE,与(1)一样可得PM=PN,∠BPM=∠BCE,∠CPN=∠CBD,则计算出∠BPM+∠CPN=120°,从而得到∠MPN=60°,于是可判断△PMN为等边三角形.
(3)利用AB﹣AD≤BD≤AB+AD(当且仅当点B、A、D共线时取等号)得到BD的最大值为4,则PN的最大值为2,然后可确定△PMN的周长的最大值.
详解:(1)如图1.
∵△ABC为等边三角形,∴AB=AC,∠ABC=∠ACB=60°.
∵AD=AE,∴BD=CE.
∵点M、N、P分别是BE、CD、BC的中点,
∴PM∥CE,PM=![]() CE,PN∥AD,PN=
CE,PN∥AD,PN=![]() BD,
BD,
∴PM=PN,∠BPM=∠BCA=60°,∠CPN=∠CBA=60°,
∴∠MPN=60°,∴△PMN为等边三角形;
故答案为:等边三角形;
(2)△PMN的形状不发生改变,仍然为等边三角形.理由如下:
连接CE、BD,如图2.
∵AB=AC,AE=AD,∠BAC=∠DAE=60°,
∴把△ABD绕点A逆时针旋转60°可得到△CAE,
∴BD=CE,∠ABD=∠ACE,
与(1)一样可得PM∥CE,PM=![]() CE,PN∥AD,PN=
CE,PN∥AD,PN=![]() BD,
BD,
∴PM=PN,∠BPM=∠BCE,∠CPN=∠CBD,
∴∠BPM+∠CPN=∠CBD+∠CBD=∠ABC﹣∠ABD+∠ACB+∠ACE=60°+60°=120°,∴∠MPN=60°,∴△PMN为等边三角形.
(3)∵PN=![]() BD,∴当BD的值最大时,PN的值最大.
BD,∴当BD的值最大时,PN的值最大.
∵AB﹣AD≤BD≤AB+AD(当且仅当点B、A、D共线时取等号)
∴BD的最大值为1+3=4,∴PN的最大值为2,∴△PMN的周长的最大值为6.