题目内容

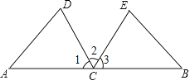
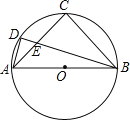
【题目】如图，已知⊙O是等腰Rt△ABC的外接圆，点D是上一点，BD交AC于点E，若BC=4，AD=，则AE的长是（　　）

A. 1 B. 1.2 C. 2 D. 3

【答案】A

【解析】利用圆周角性质和等腰三角形性质，确定AB为圆的直径，利用相似三角形的判定及性质，确定△ADE和△BCE边长之间的关系，利用相似比求出线段AE的长度即可．

∵等腰Rt△ABC，BC=4，

∴AB为⊙O的直径，AC=4，AB=4，

∴∠D=90°，

在Rt△ABD中，AD=，AB=4，

∴BD=，

∵∠D=∠C，∠DAC=∠CBE，

∴△ADE∽△BCE，

∵AD：BC=：4=1：5，

∴相似比为1：5，

设AE=x，

∴BE=5x，

∴DE=-5x，

∴CE=28-25x，

∵AC=4，

∴x+28-25x=4，

解得：x=1．

故选：A．

练习册系列答案
相关题目

【题目】甲骑摩托车从A地去B地,乙开汽车从B地去A地,同时出发,匀速行驶,各自到达终点后停止,设甲、乙两人间距离为s(单位:千米),甲行驶的时间为t(单位:小时),s与t之间的函数关系如图所示,有下列结论，其中,正确结论的个数是(　　)

①出发1小时时,甲、乙在途中相遇;

②乙开车速度是80千米/小时；

③出发1.5小时时,乙比甲多行驶了60千米;

④出发3小时时,甲、乙同时到达终点;

A. 1B. 2C. 3D. 4

【题目】野营活动中，小明用一张等腰三角形的铁皮代替锅，烙一块与铁皮形状、大小相同的饼，烙好一面后把饼翻身，这块饼能正好落在“锅”中．小丽有四张三角形的铁皮（如图所示），她想选择其中的一张铁皮代替锅，烙一块与所选铁皮形状、大小相同的饼，烙好一面后，将饼切一刀，然后将两小块都翻身，饼也能正好落在“锅”中．她的选择最多有（ ）

A. 1种B. 2种C. 3种D. 4种

【题目】（问题提出）

学习了三角形全等的判定方法（即“SAS”、“ASA”、“AAS”、“SSS”）和直角三角形全等的判定方法（即“HL”）后，我们继续对“两个三角形满足两边和其中一边的对角对应相等”的情形进行研究．

（初步思考）

我们不妨将问题用符号语言表示为：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，然后，对∠B进行分类，可分为“∠B是直角、钝角、锐角”三种情况进行探究．

（深入探究）

第一种情况：当∠B是直角时，△ABC≌△DEF．

（1）如图①，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E=90°，根据 ，可以知道Rt△ABC≌Rt△DEF．

第二种情况：当∠B是钝角时，△ABC≌△DEF．

（2）如图②，在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是钝角，求证：△ABC≌△DEF．

第三种情况：当∠B是锐角时，△ABC和△DEF不一定全等．

（3）在△ABC和△DEF，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，请你用尺规在图③中作出△DEF，使△DEF和△ABC不全等．（不写作法，保留作图痕迹）

（4）∠B还要满足什么条件，就可以使△ABC≌△DEF？请直接写出结论：在△ABC和△DEF中，AC=DF，BC=EF，∠B=∠E，且∠B、∠E都是锐角，若 ，则△ABC≌△DEF．

【题目】在平行四边形ABCD中，AE平分交边BC于E，DF平分交边BC于F．若，，则_________．

【题目】如图，在边长为1的正方形网格中建立平面直角坐标系，已知△ABC三个顶点分别为A（﹣1，2）、B（2，1）、C（4，5）．

（1）画出△ABC关于x对称的△A1B1C1；

（2）以原点O为位似中心，在x轴的上方画出△A2B2C2，使△A2B2C2与△ABC位似，且位似比为2，并求出△A2B2C2的面积．

【题目】 请同学们观察以下三个等式，并结合这些等式，回答下列问题．

（1）请你再写出另外两个符合上述规律的算式：______，______；

（2）观察上述算式，我们发现：如果设两个连续奇数分别为2n-1和2n+1(其中n为正整数)，则它们的平方差是8的倍数．请用含n的式子说明上述规律的正确性．

【题目】如图，在圆锥形的稻草堆顶点P处有一只猫，看到底面圆周上的点A处有一只老鼠，猫沿着母线PA下去抓老鼠，猫到达点A时，老鼠已沿着底面圆周逃跑，猫在后面沿着相同的路线追，在圆周的点B处抓到了老鼠后沿母线BP回到顶点P处．在这个过程中，假设猫的速度是匀速的，猫出发后与点P距离s，所用时间为t，则s与t之间的函数关系图象是（ ）

【题目】如图，C是线段AB的中点，CD平分∠ACE，CE平分∠BCD，CD=CE．

(1)求证：△ACD≌△BCE；

(2)若∠D=75°，求∠B的度数．

违法和不良信息举报电话：027-86699610 举报邮箱：58377363@163.com

精英家教网