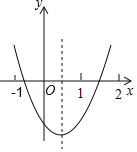Question

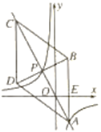
【题目】如图，在平面直角坐标系xOy中，菱形ABCD的对角线AC与BD交于点P（-1，2），AB⊥x轴于点E，正比例函数y=mx的图像与反比例函数的图像相交于A，P两点。

（1）求m，n的值与点A的坐标；

（2）求证：∽

（3）求的值

Answer 1

【答案】（1），，点的坐标是；（2）见解析；（3）.

【解析】

（1）根据点P的坐标，利用待定系数法可求出m，n的值，利用正、反比例函数图象的对称性结合点P的坐标找出点A的坐标即可解答；

（2）由菱形的性质可得出AC⊥BD，AB∥CD，利用平行线的性质可得出∠DCP=∠OAE，结合AB⊥x轴可得出∠AEO=∠CPD=90°，进而即可证出△CPD∽△AEO；

（3）由点A的坐标可得出AE，OE，AO的长，由相似三角形的性质可得出∠CDP=∠AOE，再利用正弦的定义即可求出sin∠CDB的值．

解：（1）∵正比例函数，反比例函数均经过点，

∴，，

解得：，.

∴正比例函数，反比例函数.

又正比例函数与反比例函数均是中心对称图形，则其两个交点也成中心对称点，

∵，

∴点的坐标是.

（2）证明：∵四边形ABCD是菱形，

∴AC⊥BD，AB∥CD，

∴∠DCP=∠BAP，即∠DCP=∠OAE．

∵AB⊥x轴，

∴∠AEO=∠CPD=90°，

∴△CPD∽△AEO．

（3）∵点的坐标是.

∴，，

∴，

∵，

∴△CPD∽△AEO，

∴.