题目内容
【题目】如图，在Rt△ABC中，∠BAC=90°，∠B=45°，O为BC中点，如果点M、N分别在线段AB、AC上移动，设AM的长为x，CN的长为y，且x、y满足等式
（a＞0）
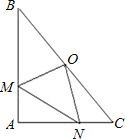
（1）求证：BM=AN；
（2）请你判断△OMN的形状，并证明你的结论；
（3）求证：当OM∥AC时，无论a取何正数，△OMN与△ABC面积的比总是定值
．
【答案】（1）证明见解析；（2）△OMN是等腰直角三角形，证明见解析；（3）证明见解析．
【解析】
试题（1）由等式可得出x=y=a，结合等腰直角三角形的性质，即可证得；
（2）作OE⊥AC，OF⊥AB，通过证明△OFM≌△OEN，可得OM=ON，根据全等三角形的性质，只要证得∠MON=90°，即可证得；
（3）当OM∥AC时，OM、ON是等腰Rt△ABC的中位线，由三角形的面积计算公式，表示出三角形的面积，比较出其比值即可；
试题解析：（1）∵∠A=90°，∠B=45°，
∴∠C=45°，从而AB=AC；
由等式
（a＞0），知x=y=a，AM=CN=a，
∴BM=AB－AM=AC－CN=AN
（2）△OMN是等腰直角三角形。证明如下：
连AO，
∵AB=AC，O为BC中点，
∴∠BAO=∠CAO=90°÷2=45°且AO⊥BC；
∵∠B=∠C=45°，
∴AO=BO=CO；
又BM=AN，
∴△BMO≌△ANO（SAS），
∴OM=ON，∠BOM=∠AON，
∴∠MON=∠AON＋∠MOA=∠BOM＋∠MOA=90°，即MO⊥NO，
故△OMN是等腰直角三角形
（3）当OM∥AC时，知∠BOM=∠A=90°，
由于∠B=45°，
∴△BMO是等腰直角三角形，从而∠BOM=45°；
∵∠MON=90°，
∴∠CON=45°，
又∠C=45°，
∴∠ONC=90°，
∵OM=ON，OB=OC，
∴且△BMO和△CNO是全等的等腰直角三角形（HL），
∴BM=MO=NO=NC=a，
由（1）知AN=BM=a，
∴AC=AB=2a，
∴△OMN与△ABC面积的比=
a2：（2a）2=
，
故结论成立
