Question

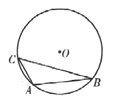
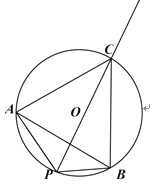
【题目】如图，A、P、B为⊙O上的三点，

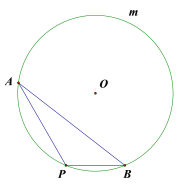
(1)在优弧AmB上求作一点C，使得 (尺规作图，保留作图痕迹，不写作法)；

(2)在(1)的条件下，若∠APB＝120°，连接AC，BC，求证：△ABC是等边三角形.

Answer 1

【答案】（1）见解析；（2）见解析.

【解析】

（1）直接作出∠APB的平分线，进而得出点C的位置；

（2）根据角平分线的性质可得∠APC=∠BPC=60°，再根据同弧或等弧所对的圆周角相等得出∠CAB=∠ABC=60°，从而得出∠ACB=60°，即可得出结论.

（1）如图：作∠APB的平分线，交⊙O于点C.

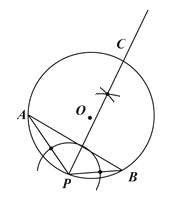
（2）∵PC平分∠APB，∠APB＝120°，

∴∠APC=∠BPC=60°，

∵∠APC与∠ABC同对弧AC，

∴∠APC=∠ABC=60°，

∵∠BPC与∠BAC同对弧BC，

∴∠BPC=∠BAC=60°，

∴∠ACB=180°-∠ABC -∠BAC=60°，

∴∠ACB=∠ABC=∠BAC，

∴AC=BC=AB，

∴△ABC是等边三角形.