题目内容
如图,已知直线AB是⊙O的切线,A为切点,OB交⊙O于点C,点D在⊙O上,且∠OBA=40°,则∠ADC= .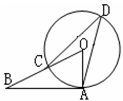

25°
先根据切线的性质判断出OA⊥AB,进而求出∠O的度数,然后根据圆心角和圆周角的关系求出∠ADC的度数.
解:∵直线AB是⊙O的切线,A为切点,
∴OA⊥AB,
∵∠OBA=40°,
∴∠O=90°-40°=50°,
又∵点D在⊙O上,
∴∠ADC= ∠O=
∠O= ×50°=25°.
×50°=25°.
本题考查了圆的切线性质、圆心角和圆周的关系及解直角三角形的知识.
解:∵直线AB是⊙O的切线,A为切点,
∴OA⊥AB,
∵∠OBA=40°,
∴∠O=90°-40°=50°,
又∵点D在⊙O上,
∴∠ADC=
 ∠O=
∠O= ×50°=25°.
×50°=25°.本题考查了圆的切线性质、圆心角和圆周的关系及解直角三角形的知识.

练习册系列答案
 快捷英语周周练系列答案
快捷英语周周练系列答案
相关题目

 ,p)时,
,p)时,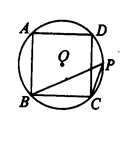

 cm
cm cm
cm
 上的两点,
上的两点, ,点D为劣弧
,点D为劣弧 的中点.
的中点.
 D是菱形;
D是菱形;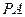 为
为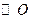 的切线,
的切线,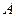 为切点,
为切点,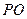 交
交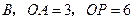 ,求
,求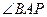 的度数.
的度数.
 内接于⊙
内接于⊙ ,若
,若 =30°,
=30°, ,则⊙
,则⊙