题目内容
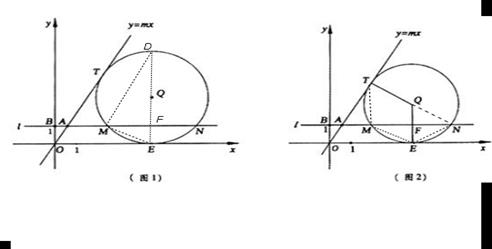
如图1,在第一象限内,直线y=mx与过点B(0,1)且平行于x轴的直线l相交于点A,半径为r的⊙Q与直线y=mx、x轴分别相切于点T、E,且与直线l分别交于不同的M、N两点.

(1)当点A的坐标为( ,p)时,
,p)时,
①填空:p=___,m= ___,∠AOE= ___.
②如图2,连接QT、QE,QE交MN于点F,当r=2时,试说明:以T、M、E、N为顶点的四边形是等腰梯形;
(2)在图1中,连接EQ并延长交⊙Q于点D,试探索:对m、r的不同取值,经过M、D、N三点的抛物线y=ax2+bx+c,a的值会变化吗?若不变,求出a的值;若变化.请说明理由.

(1)当点A的坐标为(
 ,p)时,
,p)时,①填空:p=___,m= ___,∠AOE= ___.
②如图2,连接QT、QE,QE交MN于点F,当r=2时,试说明:以T、M、E、N为顶点的四边形是等腰梯形;
(2)在图1中,连接EQ并延长交⊙Q于点D,试探索:对m、r的不同取值,经过M、D、N三点的抛物线y=ax2+bx+c,a的值会变化吗?若不变,求出a的值;若变化.请说明理由.
解:(1)1,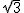 ,60°;
,60°;
(2)连接TM,ME,EN,ON,如 图,
图,
∵OE和OP是⊙Q的切线,
∴QE⊥x轴,QT⊥OT,即∠QTA=90°,
而l∥x轴,
∴QE⊥MN,
∴MF=NF,
又∵当r=2,EF=1,
∴QF=2-1=1,
∴四边形QNEM为平行四边形,即QN∥ME,
∴NQ=NE,即△QEN为等边三角形,
∴∠NQE=60°,∠QNF=30°,
在四边形OEQT中,∠QTO=∠QEO=90°,∠TOE=60°,
∴∠TQE=360°-90°-90°-60°=120°,
∴∠TQE+∠NQE=120°+60°=180 °,
°,
∴T、Q、N三点共线,即TN为直径,
∴∠TMN=90°,
∴TN∥ME,
∴∠ MTN=60°=∠TNE,
MTN=60°=∠TNE,
∴以T、M、E、N为顶点的四边形是等腰梯形;
(3)对m、r的不同取值,经过M、D、N三点的抛物线y=ax2+bx+c,a的值不会变化.理由如下:
连DM,ME,如图,
∵DM为直径,
∴∠DME=90°,
而DM垂直平分MN,
∴Rt△MFD∽Rt△EFM,
∴MF2=EF•FD,
设D(h,k),(h>0,k=2r),则过M、D、N三点的抛物线的解析式为:y=a(x-h)2+k,
又∵M、N的纵坐标都为1,
当y=1,a(x-h)2+k=1,解得x1="h-"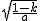 ,
, x2="h+"
x2="h+" 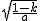 ,
,
∴MN="2"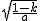 ,
,
∴MF= MN=
MN= 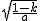 ,
,
∴(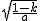 )2=1•(k-1),
)2=1•(k-1),
∵k>1,
∴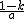 =k-1,
=k-1,
∴a=-1.
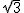 ,60°;
,60°;(2)连接TM,ME,EN,ON,如
 图,
图,
∵OE和OP是⊙Q的切线,
∴QE⊥x轴,QT⊥OT,即∠QTA=90°,
而l∥x轴,
∴QE⊥MN,
∴MF=NF,
又∵当r=2,EF=1,
∴QF=2-1=1,
∴四边形QNEM为平行四边形,即QN∥ME,
∴NQ=NE,即△QEN为等边三角形,
∴∠NQE=60°,∠QNF=30°,
在四边形OEQT中,∠QTO=∠QEO=90°,∠TOE=60°,
∴∠TQE=360°-90°-90°-60°=120°,
∴∠TQE+∠NQE=120°+60°=180
 °,
°,∴T、Q、N三点共线,即TN为直径,
∴∠TMN=90°,
∴TN∥ME,
∴∠
 MTN=60°=∠TNE,
MTN=60°=∠TNE,∴以T、M、E、N为顶点的四边形是等腰梯形;
(3)对m、r的不同取值,经过M、D、N三点的抛物线y=ax2+bx+c,a的值不会变化.理由如下:
连DM,ME,如图,
∵DM为直径,
∴∠DME=90°,
而DM垂直平分MN,
∴Rt△MFD∽Rt△EFM,
∴MF2=EF•FD,
设D(h,k),(h>0,k=2r),则过M、D、N三点的抛物线的解析式为:y=a(x-h)2+k,
又∵M、N的纵坐标都为1,
当y=1,a(x-h)2+k=1,解得x1="h-"
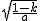 ,
, x2="h+"
x2="h+" 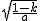 ,
,∴MN="2"
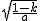 ,
,∴MF=
 MN=
MN= 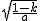 ,
,∴(
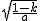 )2=1•(k-1),
)2=1•(k-1),∵k>1,
∴
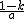 =k-1,
=k-1,∴a=-1.
略

练习册系列答案
相关题目
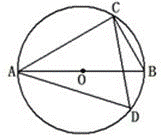
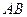 是⊙
是⊙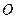 的弦,点D是弧AB的中点,过B作A
的弦,点D是弧AB的中点,过B作A B的垂线交AD的延长线于C.求证:AD=DC.
B的垂线交AD的延长线于C.求证:AD=DC.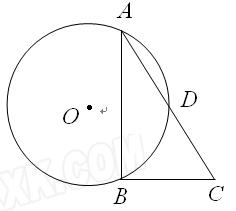
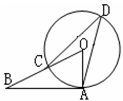
 和
和 的半径分别是5和4,
的半径分别是5和4,
 ,则
,则 ,则sin∠CBD的值等于( )
,则sin∠CBD的值等于( )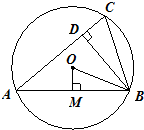

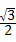

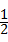

 为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第 秒.
为半径的圆在运动过程中与△ABC的边第二次相切时是出发后第 秒.
 D是AB 边上的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的延长线交于点 F .
D是AB 边上的一点,以BD为直径的⊙0与边 AC 相切于点E,连结DE并延长,与BC的延长线交于点 F . 