题目内容
【题目】已知直线AB∥CD,直线EF与AB,CD分别相交于点E,F.
(1)如图1,若∠1=60°,求∠2,∠3的度数.

(2)若点P是平面内的一个动点,连结PE,PF,探索∠EPF,∠PEB,∠PFD三个角之间的关系.
①当点P在图(2)的位置时,可得∠EPF=∠PEB+∠PFD请阅读下面的解答过程并填空(理由或数学式)
解:如图2,过点P作MN∥AB
则∠EPM=∠PEB(_______)
∵AB∥CD(已知)MN∥AB(作图)
∴MN∥CD(_______)
∴∠MPF=∠PFD (_______)
∴_____=∠PEB+∠PFD(等式的性质)
即:∠EPF=∠PEB+∠PFD
②拓展应用,当点P在图3的位置时,此时∠EPF=80°,∠PEB=156°,则∠PFD=_____度.
③当点P在图4的位置时,请直接写出∠EPF,∠PEB,∠PFD三个角之间关系_____.
【答案】(1)∠2=60°,∠3=60°;(2) 两直线平行,内错角相等 如果两条直线都和第三条直线平行,那么这两条直线也互相平行 两直线平行,内错角相等 ∠EPM+∠FPM 124 ∠EPF+∠PFD=∠PEB .
【解析】
(1)根据对顶角相等求∠2,根据两直线平行,同位角相等求∠3;
(2)①过点P作MN∥AB,根据平行线的性质得∠EPM=∠PEB,且有MN∥CD,所以∠MPF=∠PFD,然后利用等式性质易得∠EPF=∠PEB+∠PFD.
②同①;
③利用平行线的性质和三角形的外角性质得到三个角之间的关系.
(1)∵∠2=∠1,∠1=60°
∴∠2=60°,
∵AB∥CD
∴∠3=∠1=60°;
(2)①如图2,过点P作MN∥AB,则∠EPM=∠PEB(两直线平行,内错角相等)
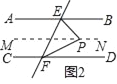
∵AB∥CD(已知),MN∥AB,
∴MN∥CD(如果两条直线都和第三条直线平行,那么这两条直线也互相平行)
∴∠MPF=∠PFD(两直线平行,内错角相等)
∴∠EPM+∠MPF=∠PEB+∠PFD(等式的性质)
即∠EPF=∠PEB+∠PFD;
故答案为:两直线平行,内错角相等;如果两条直线都和第三条直线平行,那么这两条直线也互相平行;两直线平行,内错角相等;∠EPM+∠MPF;
②过点P作PM∥AB,如图3所示:

则∠PEB+∠EPM=180°,∠MPF+∠PFD=180°,
∴∠PEB+∠EPM+∠MPF+∠PFD=180°+180°=360°,
即∠EPF+∠PEB+∠PFD=360°,
∴∠PFD=360°﹣80°﹣156°=124°;
故答案为:124;
③∠EPF+∠PFD=∠PEB.
故答案为:∠EPF+∠PFD=∠PEB.

 天天向上一本好卷系列答案
天天向上一本好卷系列答案 小学生10分钟应用题系列答案
小学生10分钟应用题系列答案【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )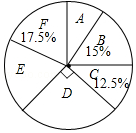
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人