题目内容
【题目】如图,已知抛物线y= ![]() x2﹣
x2﹣ ![]() x﹣2与x轴交于A,B两点(点A在点B的右边),与y轴交于点C.
x﹣2与x轴交于A,B两点(点A在点B的右边),与y轴交于点C.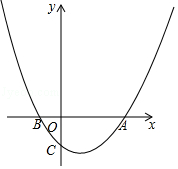
(1)求点A,B,C的坐标;
(2)点D是此抛物线上的点,点E是其对称轴上的点,求以A,B,D,E为顶点的平行四边形的面积;
(3)此抛物线的对称轴上是否存在点P,使得△ACP是等腰三角形?若存在,请求出点P的坐标;若不存在,请说明理由.
【答案】
(1)
解:令y=0得: ![]() x2﹣
x2﹣ ![]() x﹣2=0,解得x=﹣2或x=4,
x﹣2=0,解得x=﹣2或x=4,
∴A(4,0)、B(﹣2,0).
把x=0代入抛物线的解析式得:y=﹣2,
∴C(0,﹣2)
(2)
解:由题意得,抛物线的对称轴为x=1,
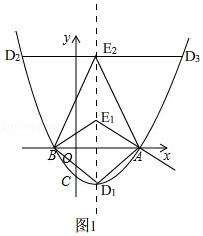
如图1,当AB为对角线时,D1为抛物线的顶点,此时四边形ADBE为菱形,
∴AB=6,DE=|2k|= ![]() ,
,
故S平行四边形ADBE= ![]() ×6×
×6× ![]() =
= ![]()
当AB为边时,DE∥AB,且DE=AB,
只能在x轴上方,有两种情况,D2(﹣5, ![]() )或D3(7,
)或D3(7, ![]() )但面积相等,
)但面积相等,
S平行四边形ABDE=6× ![]() =
= ![]() ,
,
∴以点A,B,D,E为顶点的平行四边形的面积为 ![]() 或
或 ![]()
(3)
解:此抛物线的对称轴上存在点P,使得△ACP是等腰三角形,设P(1,a),
∴AP2=a2+9,CP2=(a+2)2+1=a2+4a+5,AC2=20,
①当AP=CP时,即:a2+9=a2+4a+5,
∴a=1,
∴P1(1,1)
②当AC=CP时,即:a2+4a+5=20,
∴a=﹣2± ![]() ,
,
∴P2(1,﹣2+ ![]() ),P3(1,﹣2﹣
),P3(1,﹣2﹣ ![]() )
)
③当AC=AP时,即:a2+9=20,
∴a=± ![]() ,
,
∴P4(1, ![]() ),P5(1,﹣
),P5(1,﹣ ![]() ),
),
∴满足条件的点P的坐标为P1(1,1)、P2(1,﹣2+ ![]() ),P3(1,﹣2﹣
),P3(1,﹣2﹣ ![]() )、P4(1,
)、P4(1, ![]() ),P5(1,﹣
),P5(1,﹣ ![]() ).
).
【解析】(1)分别令y=0,x=0,即可解决问题.(2)分以AB为边和为对角线两种情况,利用面积公式即可求出平行四边形的面积.(3)先设出点P的坐标,进而表示出AP.CP.AC,再按等腰三角形的边分成三种情况,建立方程求解即可.
【考点精析】认真审题,首先需要了解二次函数的图象(二次函数图像关键点:1、开口方向2、对称轴 3、顶点 4、与x轴交点 5、与y轴交点),还要掌握二次函数的性质(增减性:当a>0时,对称轴左边,y随x增大而减小;对称轴右边,y随x增大而增大;当a<0时,对称轴左边,y随x增大而增大;对称轴右边,y随x增大而减小)的相关知识才是答题的关键.

 开心蛙状元测试卷系列答案
开心蛙状元测试卷系列答案【题目】如图,O为直线AB上一点,∠AOC=50°,OD平分∠AOC,∠DOE=90°.
(1)请你数一数,图中有多少个小于平角的角;
(2)求出∠BOD的度数;
(3)请通过计算说明OE是否平分∠BOC.