题目内容
【题目】如图,⊙O是△ABC的内切圆,切点为D,E,F,若AD、BE的长为方程![]() 的两个根,则△ABC的周长为 ______.
的两个根,则△ABC的周长为 ______.
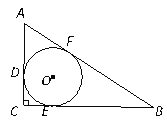
【答案】40;
【解析】求△ABC的周长,关键是求出两条直角边的长;由已知的方程可求出AF、BE的长,结合切线长定理和勾股定理,可求得CE、CF的长,进而可求出AC、BC的长;再由勾股定理求得AB,即可求△ABC的周长.
如图;
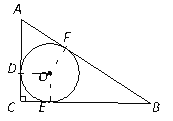
解方程![]() ,得:
,得:
x=12,x=5,
∴AD=AF=5,BF=BE=12;AB=17,
设CE=CD=x,则AC=5+x,BC=12+x;
由勾股定理,得:
AB2=AC2+BC2,即172=(5+x)2+(12+x)2,
解得:x=3(负值舍去),
∴AC=8,BC=15;
因此△ABC的周长=AC+BC+AB=8+15+17=40,.
故答案为:40.

练习册系列答案
相关题目
【题目】某校实施课程改革,为初三学生设置了A,B,C,D,E,F共六门不同的拓展性课程,现随机抽取若干学生进行了“我最想选的一门课”调查,并将调查结果绘制成如图统计图表(不完整)
选修课 | A | B | C | D | E | F |
人数 | 20 | 30 |
根据图标提供的信息,下列结论错误的是( )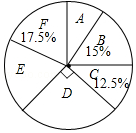
A.这次被调查的学生人数为200人
B.扇形统计图中E部分扇形的圆心角为72°
C.被调查的学生中最想选F的人数为35人
D.被调查的学生中最想选D的有55人


