题目内容
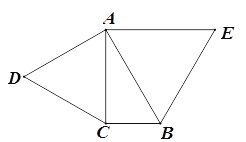
【题目】定义:如图①,点M、N把线段AB分割成AM、MN和BN,若以AM,MN、BN为边的三角形是一个直角三角形,则称点M,N是线段AB的勾股分割点.
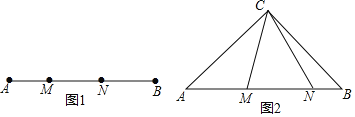
(1)已知点M、N是线段AB的勾股分割点,若AM=2,MN=3,求BN的长;
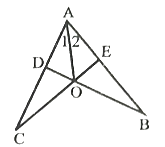
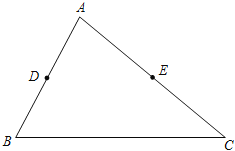
(2)如图2,在Rt△ABC中,AC=BC,点M,N在斜边AB上,∠MCN=45°,求证:点M,N是线段AB的勾股分割点(提示:把△ACM绕点C逆时针旋转90°)
(3)在(2)的前提下,若∠BCN=15°,BN=1.求AN的长.
【答案】(1)![]() 或
或![]() ;(2)见解析;(3)2+
;(2)见解析;(3)2+![]()
【解析】
(1)分两种情况讨论,根据勾股分割点定义可求BN的长;
(2)过点A作AD⊥AB,且AD=BN,由题意可证△ADC≌△BNC,可得CD=CN,∠ACD=∠BCN,可求∠MCD=∠MCN,则可证△MDC≌△MNC,可得MN=DM,根据勾股定理可得BN2+AM2=MN2,则点M,N是线段AB的勾股分割点;
(3)过点C作CD⊥AB,垂足为D,根据等腰直角三角形的性质可得AD=CD=BD,∠DBC=∠DCB=45°,可求∠DCN=∠DCB﹣∠NCB=30°,可得CD=![]() DN=BD,即可求DN=
DN=BD,即可求DN=![]() ,则可求AN的长.
,则可求AN的长.
(1)分两种情况:
①当MN为最大线段时,
∵点 M、N是线段AB的勾股分割点,
∴BN=![]() ,
,
②当BN为最大线段时,
∵点M、N是线段AB的勾股分割点,
∴BN=![]() ,
,
综上所述:BN的长为![]() 或
或![]() ;
;
(2)如图,过点A作AD⊥AB,且AD=BN,
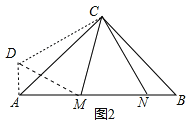
∵AD=BN,∠DAC=∠B=45°,AC=BC,
∴△ADC≌△BNC(SAS),
∴CD=CN,∠ACD=∠BCN,
∵∠MCN=45°,
∴∠DCA+∠ACM=∠ACM+∠BCN=45°,
∴∠MCD=∠MCN,且CD=CN,CM=CM,
∴△MDC≌△MNC(SAS),
∴MN=DM,
在Rt△MDA中,AD2+AM2=DM2,
∴BN2+AM2=MN2,
∴点M,N是线段AB的勾股分割点;
(3)如图,过点C作CD⊥AB,垂足为D,
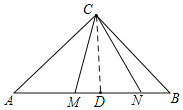
∵AC=BC,∠ACB=90°,CD⊥AB,
∴AD=CD=BD,∠DBC=∠DCB=45°,
∵∠BCN=15°,
∴∠DCN=∠DCB﹣∠NCB=30°,
∵tan∠DCN=![]() ,
,
∴CD=![]() DN,
DN,
∴DB=![]() DN,
DN,
∵NB=DB﹣DN=![]() DN﹣DN=1,
DN﹣DN=1,
∴DN=![]() ,
,
∴AD=DB=![]() DN=
DN=![]() ,
,
∴AN=AD+DN=![]() =2+
=2+![]() .
.