题目内容
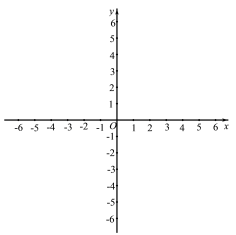
【题目】如图，正方形
的顶点
在坐标原点，正方形
的边
与
在同一直线上， 
与
在同一直线上，且
，边和边所在直线的解析式分别为： 
和
，则点
的坐标是（ ）
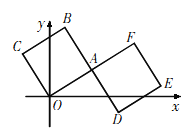
A.(6，-1)B.(7，-1)C.(7，-2)D.(6，-2)
【答案】B
【解析】
联立OA边和AB边所在直线的解析式成方程组，通过解方程组可求出点A的坐标，根据全等三角形的性质可得出点M的坐标，再求点D的坐标即可．
解：联立OA边和AB边所在直线的解析式成方程组，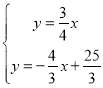
，解得：
，
∴点A的坐标为(4,3)．
如图，
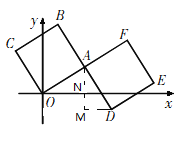
过点A作AN⊥x轴，过点D作x轴的平行线，交AN于点M，
∵∠OAM+∠MAD=90°,∠OAM+∠AON=90°，
∴∠AON=∠DAM．
在△AON和△DAM中，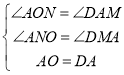
∴△AON≌△DAM(AAS)，
∴ON=AM，AN=DM，
∴点M的坐标为(4,-1),
∴点D的纵坐标为-1，
把y=-1代入
，得x=7,
∴点D的坐标为(7,-1),
故选B．
练习册系列答案
相关题目
