题目内容
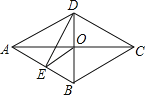
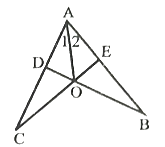
【题目】如图，
，
，垂足分别为E、D，CE，BD相交于
．
（1）若
，求证：
；
（2）若，求证：．
【答案】（1）证明见解析；（2）证明见解析．
【解析】
（1）根据已知条件，∠BEC=∠CDB=90°，∠EOB=∠DOC，所以∠B=∠C，则△ABO
△ACO（AAS），即OB=OC.
（2）根据（1）可得△BOE△COD（AAS），即OE=OD，再由CE⊥AB，BD⊥AC可得AO是∠BAC的角平分线，故∠1=∠2.
（1）∵CE⊥AB，BD⊥AC，∴∠BEC=∠CDB=90°，
又∵∠EOB=∠DOC，∴∠B=∠C，∴在△ABO与△ACO中，
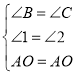，∴△ABO△ACO（AAS），∴OB=OC．
（2）由（1）知，∠BEO=∠CDO，∴在△BOE与△COD中，
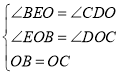，∴△BOE△COD（AAS），∴OE=OD．
又∵CE⊥AB，BD⊥AC，∴AO是∠BAC的角平分线，∴∠1=∠2．
练习册系列答案
相关题目
【题目】小明同学在用描点法画二次函数y=x2+bx+c图像时，由于粗心他算错了一个y值，列出了下面表格：
x | … | －1 | 0 | 1 | 2 | 3 | … |
y=x2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
（1）请你帮他指出这个错误的y值，并说明理由；
（2）若点M（m，y1），N（m+4，y2）在二次函数y=x2+bx+c图像上，且m＞－1，试比较y1与y2的大小．
