题目内容
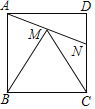
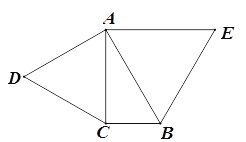
【题目】已知△ABC中, ∠ACB=90°,∠CAB=30°,以AC,AB为边向外作等边三角形ACD和等边三角形ABE,点F在AB上,且到AE,BE的距离相等.
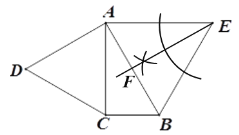
(1)用尺规作出点F; (要求:尺规作图,保留作图痕迹,不写作法)
(2)连接EF,DF,证明四边形ADFE为平行四边形.
【答案】(1)详见解析;(2)详见解析
【解析】
(1)由“点F在AB上,且到AE,BE的距离相等”可知作∠AEB的角平分线与AB的交点即为点F;
(2)先证明△ACB≌△AFE,再由全等三角形的性质得出AD∥EF,AD =EF,即可判定四边形ADFE为平行四边形.
解:(1)如图,作∠AEB的角平分线,交AB于F点
∴F为所求作的点
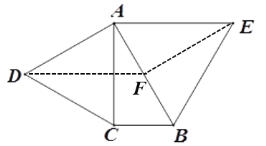
(2)如图,连接EF,DF,
∵△ABE和△ACD都是等边三角形,∠ACB=90°,∠CAB=30°,EF平分∠AEB,
∴∠DAE=150°,∠AEF=30°,
∴△ACB≌△AFE
∴∠DAE+∠AEF=180°,EF=AC
∴AD∥EF,AD=AC=EF
∴四边形ADFE为平行四边形

练习册系列答案
相关题目
【题目】小明同学在用描点法画二次函数y=x2+bx+c图像时,由于粗心他算错了一个y值,列出了下面表格:
x | … | -1 | 0 | 1 | 2 | 3 | … |
y=x2+bx+c | … | 5 | 3 | 2 | 3 | 6 | … |
(1)请你帮他指出这个错误的y值,并说明理由;
(2)若点M(m,y1),N(m+4,y2)在二次函数y=x2+bx+c图像上,且m>-1,试比较y1与y2的大小.