题目内容
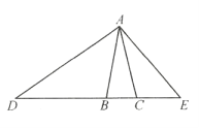
【题目】如图，在
中，
，三条内角平分线交于点
，过点作
垂线，分别交
、
于点
、
，请写出图中相似的三角形，并说明其中两对相似的理由.
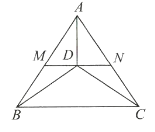
【答案】△ABD∽△ACD，△AMD∽△AND，△BMD∽△BDC∽△DNC，理由见解析
【解析】
根据角平分线和垂线的性质易证△AMD∽△AND，根据等腰三角形底角相等的性质可以判定∠ABD=∠ACD，即可证MN∥BC，进而可以证明△AMD∽△AND，△BMD∽△BDC∽△DNC，△ABD∽△ACD，即可解题．
解：△ABD∽△ACD，△AMD∽△AND，△BMD∽△BDC∽△DNC，
证明：△ABD∽△ACD，△AMD∽△AND，
∵AB=AC，
∴∠ABC=∠ACB，
∴∠ABD=∠ACD，
∵AD为角平分线，
∴△ABD∽△ACD，
∵∠ADM=∠ADN，∠BAD=∠CAD，
∴△ADM∽△ADN．
练习册系列答案
相关题目
