��Ŀ����
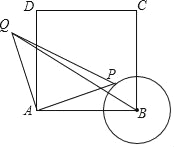
����Ŀ��ƽ��ֱ������ϵxOy�У���ԭ��O����A��0��4����C��12��0��������OABC����AOC��ƽ���߽�AB�ڵ�D����P�ӵ�O��������ÿ��2![]() ����λ���ȵ��ٶ�������OD�����ƶ���ͬʱ��Q�ӵ�O��������ÿ��4����λ���ȵ��ٶ���x���������ƶ������ƶ�ʱ��Ϊt�룮
����λ���ȵ��ٶ�������OD�����ƶ���ͬʱ��Q�ӵ�O��������ÿ��4����λ���ȵ��ٶ���x���������ƶ������ƶ�ʱ��Ϊt�룮

��1������P�ƶ�����Dʱ�������ʱt��ֵ��
��2����tΪ��ֵʱ����PQBΪֱ�������Σ�
��3����֪��O��P��Q����������߽���ʽΪy=��![]() �����Ƿ����ijһʱ��t������PQB��ij����ת180���������Ӧ����ǡ�ö����������������ϣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
�����Ƿ����ijһʱ��t������PQB��ij����ת180���������Ӧ����ǡ�ö����������������ϣ������ڣ����t��ֵ���������ڣ���˵�����ɣ�
���𰸡���1��2����2����t=2��t=5+![]() ��t=5��
��t=5��![]() ʱ����PQBΪֱ�������Σ���3������������tֵ��t1=
ʱ����PQBΪֱ�������Σ���3������������tֵ��t1=![]() ��t2=2��
��t2=2��
��������
��1�����ȸ��ݾ��ε��������DO�ij��������ó�t��ֵ��
��2��Ҫʹ��PQBΪֱ�������Σ���Ȼֻ�С�PQB=90�����PBQ=90�����������ù��ɶ����ֱ�����ó�PB2=��12��2t��2+��4��2t��2��QB2=��12��4t��2+42��PQ2=��4t��2t��2+��2t��2=8t2���ٷֱ�͡�PQB=90���͡�PBQ=90�����ۣ�������������tֵ���ɣ�
��3������������tֵ��������PQB��ij����ת180����������Ӧ����ǡ�ö������������ϣ�����ת����ΪPQ�е㣬��ʱ�ı���PBQB��Ϊƽ���ı��Σ�����ƽ���ı��ε����ʺͶԳ��Կ����t��ֵ��
�⣺��1�����ı���OABC�Ǿ��Σ�
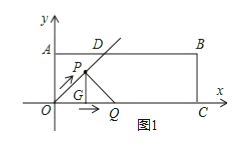
���AOC=��OAB=90�㣬
��ODƽ�֡�AOC��
���AOD=��DOQ=45�㣬
����Rt��AOD�У���ADO=45�㣬
��AO=AD=4��![]()
��![]()
��2��Ҫʹ��PQBΪֱ�������Σ���Ȼֻ�С�PQB=90�����PBQ=90�㣮
��ͼ1��
��PG��OC�ڵ�G����Rt��POG�У�
�ߡ�POQ=45�㣬
���OPG=45�㣬
��![]()
��OG=PG=2t��
���P��2t��2t��
�֡�Q��4t��0����B��12��4����
���������ľ��빫ʽ�ɵã�PB2=��12��2t��2+��4��2t��2��QB2=��12��4t��2+42��PQ2=��4t��2t��2+��2t��2=8t2��
������PQB=90��������PQ2+BQ2=PB2��
����8t2+[��12��4t��2+42]=��12��2t��2+��4��2t��2��
�����ã�t2��2t=0��
��ã�t1=0����ȥ����t2=2��
��t=2��
������PBQ=90��������PB2+QB2=PQ2��
��[��12��2t��2+��4��2t��2]+[��12��4t��2+42]=8t2��
�����ã�t2��10t+20=0��
��ã�![]()
�൱t=2��![]() ��
��![]() ʱ����PQBΪֱ�������Σ�
ʱ����PQBΪֱ�������Σ�
��3������������tֵ���������£�
����PQB��ij����ת180����������Ӧ����ǡ�ö������������ϣ�
����ת����ΪPQ�е㣬��ʱ�ı���PBQB��Ϊƽ���ı��Σ�
��PO=PQ����P��2t��2t����Q��4t��0����֪��ת��������ɱ�ʾΪ��3t��t����
�ߵ�B����Ϊ��12��4����
���B����������6t��12��2t��4����
����![]() �ã�2t2��13t+18=0��
�ã�2t2��13t+18=0��
��ã�![]()

����Ŀ��������������Ƶ�����г��Ϸ������ֳ���������ijҽҩ��˾ÿ�¹̶������ס��������ͺŵķ��������ֹ�20��ֻ�������в�Ʒ����ȫ���۳���ԭ�ϳɱ������۵��ۼ�����������������
| �� | �� |
ԭ�ϳɱ� | 12 | 8 |
���۵��� | 18 | 12 |
������� | 1 | 0.8 |
��1�����ù�˾���·ݵ���������Ϊ300��Ԫ����ס��������ͺŵIJ�Ʒ�ֱ��Ƕ�����ֻ��
��2����˾ʵ�мƼ������ƣ�������ÿ����һֻ���ֻ��һ��������ɣ������˾���·�Ͷ���ܳɱ���ԭ���ܳɱ�+��������ܶ������239��Ԫ��Ӧ�������żס��������ͺŵIJ�������ʹ���¹�˾�������������������������=�������멁Ͷ���ܳɱ���
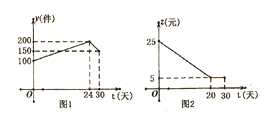
����Ŀ�����괺�������ظɺ���ij����������ˮ���ţ�ÿ������������������ˮ120�֣��йز��Ž������𣬴Ӽס�����ˮ����������ˮ��������ˮ�㣬�׳�ÿ�����ɵ���80�֣��ҳ�ÿ�����ɵ���90�֣�����ˮ����ˮ��������ˮ���·�̺��˷����±���
��������ˮ���·�̣�ǧ�ף� | �˷ѣ�Ԫ/����ǧ�ף� | |
�׳� | 20 | 12 |
�ҳ� | 14 | 15 |
��1����ij�����ˮ�����˷�Ϊ26700Ԫ����Ӽס�����ˮ�������˶��ٶ�����ˮ��
��2����Ӽ׳���������ˮ![]() �֣����˷�ΪWԪ����д��W������
�֣����˷�ΪWԪ����д��W������![]() �ĺ�����ϵʽ���������ŵ��˷�������ʹÿ������˷���ʡ��
�ĺ�����ϵʽ���������ŵ��˷�������ʹÿ������˷���ʡ��