��Ŀ����
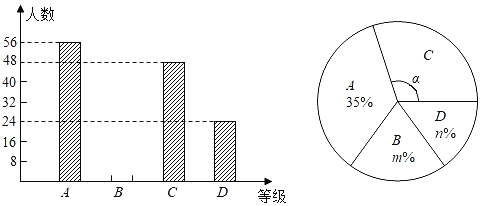
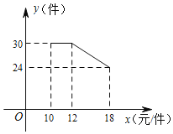
����Ŀ�� ij��������һ�ֲ�Ʒ�����ֲ�Ʒ�ijɱ���Ϊ10Ԫ/������֪���ۼ۲����ڳɱ��ۣ�����۲��Ź涨���ֲ�Ʒ�����ۼ۲�����18Ԫ/���г����鷢�֣��ò�Ʒÿ���������y�����������ۼ�x��Ԫ/����֮��ĺ�����ϵ��ͼ��ʾ��
��1����12��x��18ʱ����y��x֮��ĺ�����ϵʽ��
��2����ÿ�����������w��Ԫ�������ۼ�x��Ԫ/����֮��ĺ�����ϵʽ�����ÿ�����ۼ�Ϊ����Ԫʱ��ÿ����������������������Ƕ��٣�
���𰸡���1��y����x+42��12��x��18������2��w��![]() ����x��18Ԫʱ����������������������192Ԫ
����x��18Ԫʱ����������������������192Ԫ
��������
��1���������⣬����ͼ�����ô���ϵ�������������������y�����������ۼ�x��Ԫ/����֮��ĺ�����ϵʽ��
��2��������������=�����������ۼ�-���ۣ����г�ÿ�����������w��Ԫ�������ۼ�x��Ԫ/����֮��ĺ�����ϵʽ�������ݺ���������������������
�⣺��1�������⣬��y��x֮��ĺ�����ϵʽΪ��y��kx+b
���㣨12��30����18��24�������
![]() �����
�����![]()
�൱12��x��18ʱ�� y��x֮��ĺ�����ϵʽ��y����x+42��12��x��18��
��2�������⣬��w��y��x��10��
����w��![]()
��10��x��12ʱ���������Ϊw��60Ԫ
��12��x��18ʱ�� w����x2+52x��420������x��26��2+256
��a����1��0
�������߿������£��ʵ�12��x��18ʱ��w��x�����������
�൱x��18ʱ�������ֵ��w��192Ԫ
�ʵ�x��18Ԫʱ����������������������192Ԫ����ʱ���۵ļ���Ϊ24����

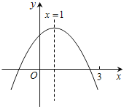
����Ŀ�����κ���y��ax2+bx+c��a��b��cΪ��������a��0���е�x��y�IJ��ֶ�Ӧֵ�����
x | ��1 | 0 | 1 | 3 |
y | ��1 | 3 | 5 | 3 |
���н��۴�����ǣ�������
A.ac��0
B.��x��1ʱ��y��ֵ��x���������С
C.3�Ƿ���ax2+��b��1��x+c��0��һ����
D.����1��x��3ʱ��ax2+��b��1��x+c��0