Question

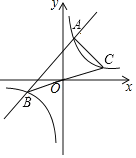
【题目】如图，已知函数的图象与函数的图象交于、两点，连接并延长交函数的图象于点，连接，若的面积为12，则的值为______．

Answer 1

【答案】

【解析】

连接OA，根据反比例函数的对称性可得OB=OC，那么S△OAB=S△OAC=S△ABC=6，求出直线y=x+3与y轴交点D的坐标，设A（a，a+3），B（b，b+3），则C（-b，-b-3），根据S△OAB=6，得出a-b=4①．根据S△OAC=6，得出-a-b=3②，①与②联立，求出a、b的值，即可求解．

解：如图，连接OA．
由题意，可得OB=OC，根据△ABC的面积为12，
∴S△OAB=S△OAC=S△ABC=6，
设直线y=x+3与y轴交于点D，则D（0，3），
设A（a，a+3），B（b，b+3），则C（-b，-b-3），
∴S△OAB=×3×（a-b）=6，
∴a-b=4①，
过A点作AM⊥x轴于点M，过C点作CN⊥x轴于点N，
则S△OAM=S△OCN=k，
∴S△OAC=S△OAM+S梯形AMNC-S△OCN=S梯形AMNC=6，

∴（-b-3+a+3）（-b-a）=6，
将①代入，得
∴-a-b=3②，
①+②，得-2b=7，b=-，
①-②，得2a=1，a=，
∴A（，），
∴k=×=．
故答案为．