��Ŀ����
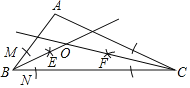
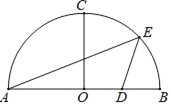
����Ŀ����ͼ��AB�ǰ�ԲO��ֱ�����뾶OC��AB��OB��4��D��OB���е㣬��E�ǻ�BC�ϵĶ��㣬����AE�� DE��
��1������E�ǻ�BC���е�ʱ������ADE�������
��2����tan��AED��![]() ����AE�ij���
����AE�ij���
��3����F�ǰ뾶OC��һ���㣬���E��ֱ��OC�ľ���Ϊm��
�ٵ���DEF�ǵ���ֱ��������ʱ����m��ֵ��
���ӳ�DF����Բ���ڵ�G������AG����EG��AG��DE��ֱ��д��DE�ij��� ����
���𰸡���1��6![]() ����2��
����2��![]() ��3����
��3����![]() ��
��![]()
��������
��1����Ϊ��E�ǻ�BC���е㣬����OE��BE������45������ֱ�������Σ����á�AEB����Ӱ�������۽������̼��ɣ�
��2�������������Ǻ�����������DF��AE����ֱ�������Σ����ų���ƽ�����ƣ�����AD��AB֮�ȣ���ʾAF���á�AFD�������ɹ�ϵ���̣�
��3���ٷֱ���D��E��FΪֱ�Ƕ˵�������ۣ���K��ȫ�Ⱥ���Ӱ�������۽���������⣮
����Ҫ����֤����BDEΪ���������Σ��ù��ɶ������AG���á�AOG����DEB���DE
�⣺��1����ͼ����EH��AB������OE��EB
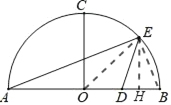
��DH��a����HB��2��a��OH��2+a
�ߵ�E�ǻ�BC�е�
���COE����EOH��45��
��EH��OH��2+a
��Rt��AEB��EH2��AHBH
��2+a��2����6+a����2��a��
���a��![]()
��a��![]() ��
��
S��ADE��![]()
��2����ͼ����DF��AE������ΪF������BE
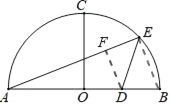
��EF��2x��DF��3x
��DF��BE
��![]()
��![]() ��3
��3
��AF��6x
��Rt��AFD��AF2+DF2��AD2
��6x��2+��3x��2����6��2
���x��![]()
AE��8x��![]() .
.
��3����I.����DΪ����ֱ��������ֱ�Ƕ���ʱ����ͼ
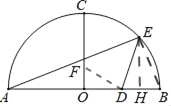
��DH��a
��֤��ODF����EDH
��OD��EH��2
��Rt��ABE��EH2��AHBH
22����6+a����2��a��
���a��![]() ��a=
��a=![]() (����������ȥ)
(����������ȥ)
��DH=![]() �� m��OH =
�� m��OH =![]()
II.����EΪ����ֱ��������ֱ�Ƕ���ʱ����ͼ
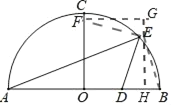
��֤��EFG�ա�EDH
��DH��a����GE��a��EH��CG��2+a
��Rt��ABE��EH2��AHBH
��2+a��2����6+a����2��a��
���a��![]() ��a=
��a=![]() (����������ȥ)
(����������ȥ)
��DH=![]() �� m��OH =
�� m��OH =![]()
III.����FΪ����ֱ��������ֱ�Ƕ���ʱ����ͼ
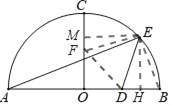
��֤��EFM�ա�ODF
��OF��a����ME��a��MF��OD��2
��EH��a+2��
��Rt��ABE��EH2��AHBH��
��a+2��2����4+a����4��a����
���a��![]() ��a=
��a=![]() ������������ȥ����
������������ȥ����
m��![]() ��
��
����������m��ֵΪ![]() ��
��![]() ��
��![]() .
.
����֤��BDEΪ���������Σ�
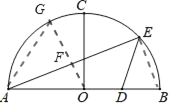
BD��BE��2��
����AOF����ABE��
��OF��1��
��Rt��OFA�У��ɹ��ɶ����ɵ�AF��![]() ��
��
GF��3��
���ɶ����ɵ�AG��![]() ��
��
����AOG����DEB
��![]() ��
��
��DE��![]()

����Ŀ�����ۿ���ij���л���Ϊ���˽���У�������Ķ���ѧ�̿������״�������ȡijУ���ֳ���ѧ�����е��飮�������е������ݻ��Ƴ����²�������ͳ��ͼ���������ͼ���е���Ϣ����������⣺
��� | ���� | ռ�������ı��� |
���� | a | 0.3 |
һ�� | 57 | 0.38 |
������ | b | c |
˵����� | 9 | 0.06 |

(1)������������������a��b��c��ֵ������ȫͳ��ͼ��
(2)�ٸ��������ͳ�ƽ����̸̸��Ը�У�������Ķ���ѧ�̿������״�Ŀ��������飻
�����Ҫ�˽�ȫʡ�������Ķ���ѧ�̿�������������ΪӦ����ν��г�����