��Ŀ����
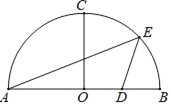
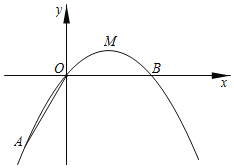
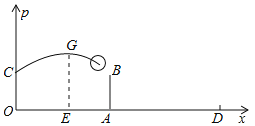
����Ŀ��Ϊ��ͼ����֪Ů���ij���ODΪ18�ף�λ�������ߴ�������AB�ĸ߶�2.24�ף�һ��Ավ�ڵ�O����������ӵ�O�����Ϸ�2��C������ǰ����ȥ������ķ���·���������ߵ�һ���֣����������������O��ˮƽ����OEΪ6��ʱ��������ߵ�G����OΪԭ�㽨����ͼ��ʾ��ƽ��ֱ������ϵ��
��1�����������е����߶�Ϊ2.8�ף���������еĸ߶�p����λ���ף���ˮƽ����x����λ���ף�֮��ĺ�����ϵʽ����Ҫ��д�Ա���x��ȡֵ��Χ����
��2���ڣ�1���������£�������������ܹ�����������ܹ��������Ƿ����磿��˵�����ɣ�
��3��������ͬѧ����Ҫ���������ʹ������磨����ѹ������û���磩����κ����ж�����ϵ�������ֵ��
���𰸡���1��p��![]() ��x��6��2+2.8;��2��������;��3��
��x��6��2+2.8;��2��������;��3��![]() .
.
��������
��1�����������ߵĶ�������Ϊ��6��2.8�������㣨0��2���������ʽ�������
��2�����õ�x��9ʱ��x��18ʱ���ֱ����pֵ�����ж�
��3���������ߵĽ���ʽΪ��p��a��x��6��2+h������C���룬��ʱ�����ߵĽ���ʽΪp��a��x��6��2+2��36a���ٸ���x��9ʱ��p��2.24����x��18ʱ��p��0�����ɵ�a�ķ�Χ���Ӷ�ȡ�����ֵ��
�⣺
��1�����������е����߶�Ϊ28�ף���������GΪ��6��2.8�������������ߵĽ���ʽΪp��a��x��6��2+2.8
�ߵ�C����Ϊ��0��2������C����������
��2��a��0��6��2+2.8
���a����![]()
��p��-![]() ��x��6��2+2.8
��x��6��2+2.8
��������еĸ߶�p����λ���ף���ˮƽ����x����λ���ף�֮��ĺ�����ϵʽ��p��-![]() ��x��6��2+2.8
��x��6��2+2.8
��2����x��9ʱ��
p��-![]() ��9��6��2+2.8��2.6��2.24
��9��6��2+2.8��2.6��2.24
��x��18ʱ��
p��-![]() ��18��6��2+2.8����0.4��0
��18��6��2+2.8����0.4��0
����η�����Թ����Ҳ����߽�
��3���������ߵĽ���ʽΪ��p��a��x��6��2+h��
����C����ã�36a+h��2����h��2��36a
���ʱ�����ߵĽ���ʽΪ
p��a��x��6��2+2��36a
�������⣬�����߽�ʱ�У�a��18��6��2+2��36a��0�����a��-![]()
Ҫʹ���������a��9��6��2+2��36a��2.24�����a��![]()
������ͬѧ����Ҫ���������ʹ������磨����ѹ������û���磩���κ����ж�����ϵ�������ֵΪ![]()

����Ŀ����ѧУ��֯�ġ�ѧϰǿ�����Ķ�֪ʶ�����У�ÿ��μӱ�����������ͬ���ɼ���ΪA��B��C��D�ĸ��ȼ���������Ӧ�ȼ��ĵ÷����μ�Ϊ100�֣�90�֣�80�ֺ�70�֣��꼶�鳤����ʦ��901���902��ijɼ��������������Ƴ����µ�ͳ��ͼ��
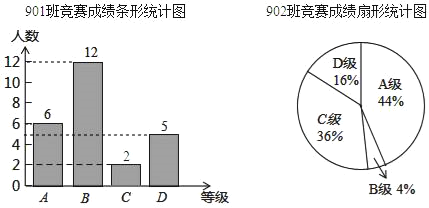
(1)�ڱ��ξ����У�902��C�������ϵ������ж��٣�
(2)���㽫����ı���������
ƽ����(��) | ��λ��(��) | ����(��) | B������������ | |
901�� | 87.6 | 90 | �� �� | 18 |
902�� | 87.6 | �� �� | 100 | �� �� |
(3)�����901���902���ڱ��ξ����еijɼ����бȽϣ�